Chapter VIII INITIAL NUCLEAR RADIATION
NATURE OF NUCLEAR RADIATIONS
NEUTRONS AND GAMMA RAYS
8.01 As stated in Chapter I, one of the special features of a nuclear explosion is the emission of nuclear radiations. These radiations, which are quite different from the thermal radiation discussed in the preceding chapter, consist of gamma rays, neutrons, beta particles, and a small proportion of alpha particles. Most of the neutrons and part of the gamma rays are emitted in the fission and fusion reactions, i.e., simultaneously with the explosion. The remainder of the gamma rays are produced in various secondary nuclear processes, including decay of the fission products. The beta particles are also emitted as the fission products decay. Some of the alpha particles result from the normal radioactive decay of the uranium or plutonium which has escaped fission in the weapon, and others (helium nuclei) are formed in fusion reactions (§ 1.69).
8.02 Because of the nature of the phenomena associated with a nuclear explosion, either in the air or near the surface, it is convenient, for practical purposes, to consider the nuclear radiations as being divided into two categories, namely, initial and residual (§ 1.02). The line of demarcation is somewhat arbitrary, but it may be taken as about l minute after the explosion, for the reasons given in § 2.43. The initial nuclear radiation, with which the present chapter will be concerned, consequently refers to the radiation emitted within 1 minute of the detonation. For underground or underwater explosions, it is less meaningful to separate the initial from the residual nuclear radiation (§ 2.82, 2.100), although the distinction may be made if desired.
8.03 The ranges of alpha and beta particles are comparatively short and they cannot reach the surface of the earth from an air burst. Even when the fireball touches the ground, the alpha and beta particles are not very important. The initial nuclear radiation may thus be regarded as consisting only of the gamma rays and neutrons produced during a period of l minute after the nuclear explosion. Both of these nuclear radiations, although different in character, can travel considerable distances through the air. Further, both gamma rays and neutrons can produce harmful effects in living organisms (see Chapter XII). It is the highly injurious nature of these nuclear radiations, combined with their long range, that makes them such a significant aspect of nuclear explosions. The energy of the initial gamma rays and neutrons is only about 3 percent of the total explosion energy, compared with some 35 to 45 percent appearing as thermal radiation in an air burst, but the nuclear radiations can cause a considerable proportion of the casualties. Nuclear radiation can also damage certain electronic equipment, as will be seen later in this chapter.
8.04 Most of the gamma rays accompanying the actual fission process are absorbed by the weapon materials and are thereby converted into other forms of energy. Thus, only a small proportion (about 1 percent) of this gamma radiation succeeds in penetrating any distance from the exploding weapon, but there are several other sources of gamma radiation that contribute to the initial nuclear radiation. Similarly, many of the neutrons produced in fission and fusion reactions (§ 1.69) are reduced in energy and captured by the weapon residues or by the air through which they travel. Nevertheless, a sufficient number of high-energy neutrons escape from the explosion region to represent a significant hazard at considerable distances away.
COMPARISON OF NUCLEAR WEAPON RADIATIONS
8.05 Although shielding from thermal radiation at distances not too close to the point of the explosion of a nuclear weapon is a fairly simple matter, this is not true for gamma rays and neutrons. For example, at a distance of 1 mile from a 1-megaton explosion, the initial nuclear radiation would probably prove fatal to a large proportion of exposed human beings even if surrounded by 24 inches of concrete; however, a much lighter shield would provide complete protection from thermal radiation at the same location. The problems of shielding from thermal and nuclear radiations are thus quite distinct.
8.06 The effective injury ranges of these two kinds of nuclear weapon radiation may also differ widely. For explosions of moderate and large energy yields, thermal radiation can have harmful consequences at appreciably greater distances than can the initial nuclear radiation. Beyond about 1¼ miles, the initial nuclear radiation from a 20-kiloton air burst, for instance, would not cause observable injury even without protective shielding. However, exposure to thermal radiation at this distance could produce serious skin burns. On the other hand, when the energy of the nuclear explosion is relatively small, e.g., a few kilotons, the initial nuclear radiation has the greater effective range.
8.07 In the discussion of the characteristics of the initial nuclear radiation, it is desirable to consider the neutrons and the gamma rays separately. Although their ultimate effects on living organisms are much the same, the two kinds of nuclear radiations differ in many respects. The subject of gamma rays will be considered in the section which follows, and neutrons will be discussed in § 8.49 et seq.
GAMMA RAYS
SOURCES OF GAMMA RAYS
8.08 In addition to the gamma rays that actually accompany the fission process, contributions to the initial nuclear radiations are made by gamma rays from other sources. Of the neutrons produced in fission, some serve to sustain the fission chain reaction, others escape, and a large number are inevitably captured by nonfissionable nuclei. Similar interactions occur for the neutrons produced by fusion. As a result of neutron capture, the nucleus is converted into a new species known as a “compound nucleus,” which is in a high-energy (or excited) state. The excess energy may then be emitted, almost instantaneously, as gamma radiations. These are called “capture gamma rays,” because they are the result of the capture of a neutron by a nucleus. The process is correspondingly referred to as “radiative capture.”
8.09 The interaction of weapon neutrons with certain atomic nuclei provides another source of gamma rays. When a “fast” neutron, i.e., one having a large amount of kinetic energy, collides with such a nucleus, the neutron may transfer some of its energy to the nucleus, leaving the latter in an excited (high-energy) state. The excited nucleus can then return to its normal energy (or ground) state by the emission of the excess energy as gamma rays. This type of interaction of a fast neutron with a nucleus is called “inelastic scattering” and the accompanying radiations are referred to as “inelastic scattering gamma rays.”1 The fast neutrons produced during the fission and fusion reactions can undergo inelastic scattering reactions with atomic nuclei in the air as well as with nuclei of weapon materials.
8.10 During the fission process, certain of the fission products and weapon products are formed as isomers.2 Some of the isomers decay initially by emitting a gamma ray. This is generally followed by emission of a beta particle that may or may not be accompanied by additional gamma rays. The initial gamma rays emitted by such isomers may be considered an independent source of gamma rays. Those gamma rays that may be emitted subsequently are generally considered to be part of the fission product decay.
8.11 Neutrons produced during the fission and fusion processes can undergo radiative capture reactions with nuclei of nitrogen in the surrounding atmosphere as well as with nuclei of various materials present in the weapon. These reactions are accompanied by (secondary) gamma rays which form part of the initial nuclear radiation. The interaction with nitrogen nuclei is of particular importance, since some of the gamma rays thereby produced have very high energies and are, consequently, much less readily attenuated than the other components of the initial gamma radiation.
8.12 The gamma rays produced during fission and as a result of neutron interactions with weapon materials form a pulse of extremely short duration, much less than a microsecond ( § 1.54 footnote). For this reason, the radiations from these sources are known as the “prompt” or “instantaneous” gamma rays.
8.13 The fission fragments and many of their decay products are radioactive species, i.e radionuclides (§ 1.30), which emit gamma radiation (see Chapter I). The half-lives of these radioactive species range from a fraction of a second to many years. Nevertheless, since the decay of the fission fragments commences at the instant of fission and since, in fact, their rate of decay is greatest at the beginning, there will be an appreciable liberation of gamma radiation from these radionuclides during the first minute after the explosion. In other words, the gamma rays emitted by the fission products make a significant contribution to the initial nuclear radiation. However, since the radioactive decay process is a continuing (or gradual) one, spread over a period of time which is long compared to that in which the instantaneous radiation is produced, the resulting gamma radiations, together with part of the gamma radiations that arise from initial isomeric decays and interactions of neutrons with nuclei of the air, are referred to as “delayed” gamma rays.
8.14 The calculated time dependence of the gamma-ray output of a hypothetical nuclear weapon is shown in Fig. 8.14. The energy rate is expressed in terms of million electron volts (§ 1.43) per second per kiloton of explosion energy. The gamma rays that result from neutron capture in nitrogen occur at late times relative to some of the other sources because the probability of capture is much greater for low-energy neutrons, i.e., those that have lost energy by multiple scattering reactions. The dashed lines in Fig. 8.14 show the gamma-ray source as it would exist in a vacuum, e.g., from an explosion above the normal atmosphere. The gamma rays that result from inelastic scattering of neutrons by nuclei of air atoms and capture in nitrogen would be absent from such an explosion.
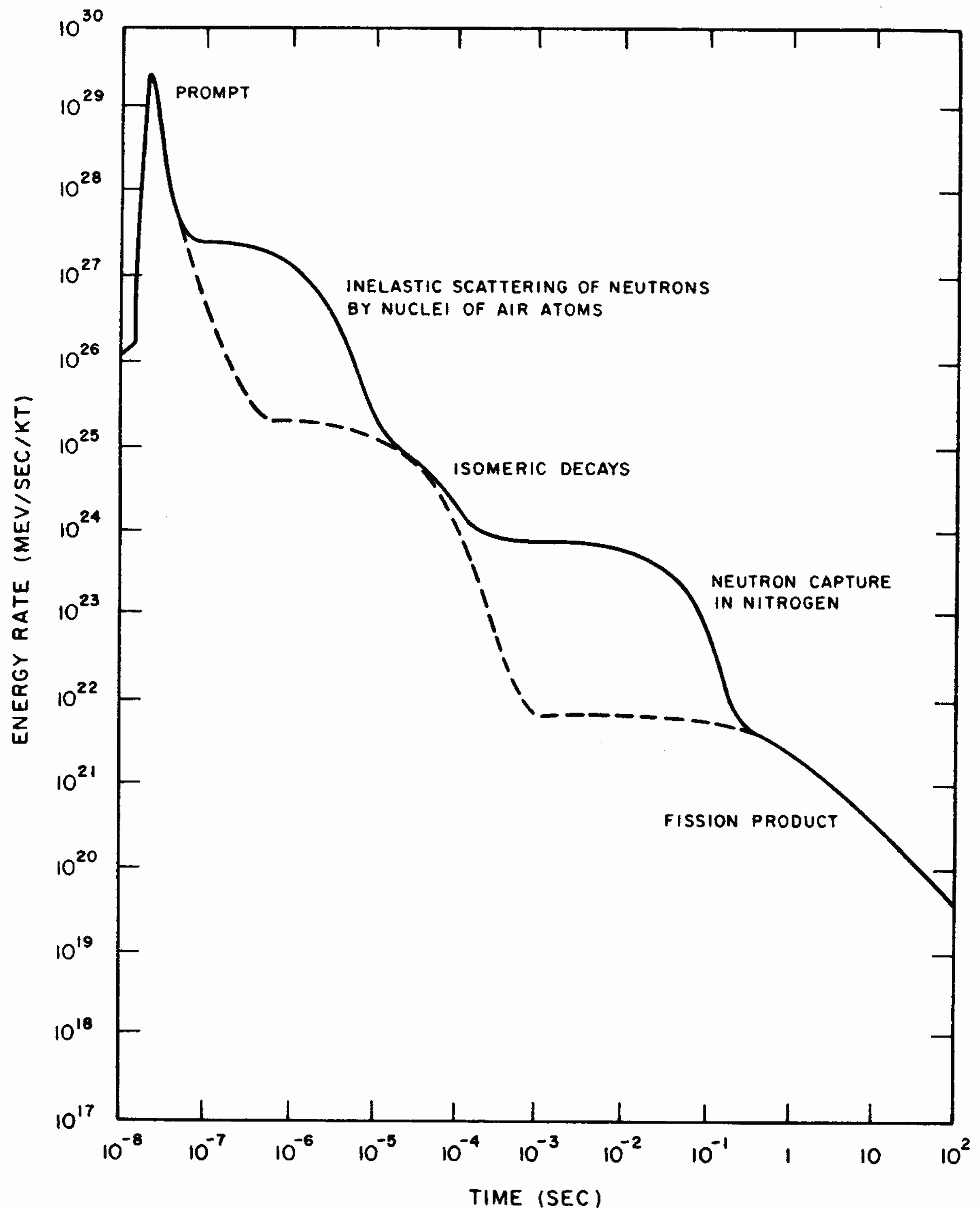
8.15 The instantaneous gamma rays and the portion of the delayed gamma rays included in the initial radiation are produced in nearly equal amounts, but they are by no means equal fractions of the initial nuclear radiation escaping from the exploding weapon. The instantaneous gamma rays are produced almost entirely before the weapon has completely blown apart. They are, therefore, strongly absorbed by the dense weapon materials, and only a small proportion actually emerges. The delayed gamma rays, on the other hand, are mostly emitted at a later stage in the explosion, after the weapon materials have vaporized and expanded to form a tenuous gas. These radiations thus suffer little or no absorption before emerging into the air. The net result is that, at a distance from an air (or surface) burst, the delayed gamma rays, together with those produced by the radiative capture of neutrons by the nitrogen in the atmosphere, contribute about a hundred times more energy than the prompt gamma rays to the total nuclear radiation received during the first minute after detonation (§ 8.47).
8.16 There is another possible source of gamma rays which may be mentioned. If a nuclear explosion occurs near the earth’s surface, the emitted neutrons can cause what is called “induced radioactivity” in the materials present in the ground (or water). This may be accompanied by the emission of gamma rays which will commence at the time of the explosion and will continue thereafter. However, except near ground zero, where the intensity of gamma rays from other sources is very high in any event, the contribution of induced radioactivity to the initial gamma radiation is small. Consequently, the radioactivity induced in the earth’s surface by neutrons will be treated in the next chapter as an aspect of the residual nuclear radiation (§ 9.31 et. seq.).
RADIATION DOSE AND DOSE RATE
8.17 Gamma rays are electromagnetic radiations analogous to X rays, but, generally of shorter wavelength or higher photon energy (§ 1.74). A measurement unit that is used specifically for gamma rays (and X rays) is called the “roentgen.” It is based on the ability of these radiations to cause ionization and produce ion pairs, i.e., separated electrons and positive ions, in their passage through matter, as described in § 1.38. In simple terms, a roentgen is the quantity of gamma radiation (or X rays) that will give rise to the formation of 2.08 × 109 ion pairs per cubic centimeter of dry air at S.T.P., i.e., at standard temperature (0°C) and pressure (1 atmosphere). This is equivalent to the release of about 88 ergs of energy when 1 gram of dry air under S.T.P. conditions is exposed to 1 roentgen of gamma radiation.3
8.18 The roentgen is a measure of exposure to gamma rays (or X rays). The effect on a biological system, such as the whole body or a particular organ, or on a material, e.g., in electronic equipment, however, is related to the amount of energy absorbed as a result of exposure to radiation. The unit of energy absorption, which applies to all kinds of nuclear radiations, including alpha and beta particles and neutrons as well as gamma rays, is the “rad.” The rad represents the deposition of l00 ergs of radiation energy per gram of the absorbing material. In stating the quantity (or dose) of a particular radiation in rads, the absorbing material must be specified since the extent of energy deposition depends on the nature of the material. In tissue at or near the surface of the body, the gamma (or X-ray) exposure of 1 roentgen results in an absorption of approximately 1 rad,4 but this rough equivalence does not necessarily apply to other materials. Furthermore, the relationship does not hold for absorption in tissue in the interior of the body. However, in describing the biological effects of nuclear radiations in this book, the energy absorption (in rads) refers to that in tissue at (or close to) the body surface nearest to the explosion(§ 12.108).
8.19 There are two basic types of nuclear radiation measurement both of which are important for biological effects and damage to materials. One is the total “exposure” in roentgens of gamma rays or the total absorbed “dose” in rads of any radiation accumulated over a period of time. The other is the “exposure rate” or the “dose rate”, respectively; the rate is the exposure or the absorbed dose received per unit time. Exposure rates may be expressed in roentgens per hour or, for lower rates, in milliroentgens per hour, where 1 milliroentgen is one thousandth part of a roentgen. Absorbed dose rates can be given correspondingly in rads per hour or millirads per hour. In connection with damage to electronic equipment, the exposure rates are generally stated in roentgens per second and the absorbed dose rates in rads per second.
MEASUREMENT OF GAMMA RADIATION
8.20 Thermal radiation from a nuclear explosion can be felt (as heat), and the portion in the visible region of the spectrum can be seen as light. The human senses, however, do not respond to nuclear radiations except at very high intensities (or dose rates), when itching and tingling of the skin are experienced. Special instrumental methods, based on the interaction of these radiations with matter, have therefore been developed for the detection and measurement of various nuclear radiations. Some of the instruments described below respond to neutrons (to a certain extent) as well as to gamma rays. For gamma-ray measurement, the instrument would have to be shielded from neutrons. The basic operating principles of the instruments are described below and their use for determining either doses or dose rates is indicated in §§ 8.29, 8.30.
8.21 Normally a gas will not conduct electricity to any appreciable extent, but as a result of the formation of ion pairs, by the passage of nuclear (or ionizing) radiations, e.g., alpha particles, beta particles or gamma rays, the gas becomes a reasonably good conductor. Several types of ionization instruments, e.g., the Geiger counter and the pocket chamber (or dosimeter), for the measurement of gamma (and other) radiations, are based on the formation of electrically charged ion pairs in a gas and its consequent ability to conduct electricity.
8.22 Semiconductor (solid-state) detectors depend on ionization in a solid rather than in a gas. These detectors consist of three regions: one is the n (for negative) region, so called because it has an excess of electrons available for conducting electricity, the second is the p (for positive) region which has a deficiency of such electrons, and the third is neutral. In the detector, the neutral region is located between the n and p regions. A voltage from a battery is applied across the detector to balance the normal difference of potential between the outer regions and there is no net flow of current. When exposed to nuclear radiation, ionization occurs in the neutral region and there is a pulse of current proportional to the radiation intensity. Semiconductor detectors for operation at normal temperature are made of silicon which is either pure (neutral region) or contains regulated amounts of impurities, e.g., arsenic or antimony (n region) or boron or aluminum (p region).
8.23 Another type of interaction of nuclear radiations with matter, either solid, liquid, or gas, called “excitation,” is also used in radiation measurement. Instead of the electron being removed completely from an atom, as it is in ionization, it acquires an additional amount of energy. As a result, the atom is converted into a high-energy (or excited) electronic state. When an atom (or molecule) becomes electronically excited, it will generally give off the excess (or excitation) energy within about one-millionth of a second. Certain materials, usually in the solid or liquid state, are able to lose their electronic excitation energy in the form of visible flashes of light or scintillations. In scintillation detectors, the scintillations are counted by means of a photomultiplier tube and associated electronic devices.
8.24 In radio-photoluminescent dosimeters, irradiation produces stable fluorescence centers which can be stimulated by subsequent ultraviolet illumination to emit visible light. For example, after exposure to gamma (or X) rays, a silver metaphosphate glass rod or plate system emits a phosphorescent glow when subjected to ultraviolet light; the glow can be measured by means of a photoelectric detector. In thermoluminescent dosimeters metastable centers are produced by radiation, and these centers can be induced to emit light by heating the material. A thermoluminescent substance commonly used in radiation dosimeters is lithium fluoride containing a small quantity of manganese. The total light emission from radio-photolumine scent and thermoluminescent dosimeters is a measure of the absorbed dose in the sensitive material.
8.25 In most materials, the energy of the absorbed radiation ultimately appears in the form of heat. Thus, the heat generated by the passage of radiation is a measure of the absorbed dose. This fact is utilized in a special calorimeter dosimeter consisting of a thin sample of absorbing material. The energy deposited by the radiation can then be determined from the measured temperature rise and the known heat capacity of this material.
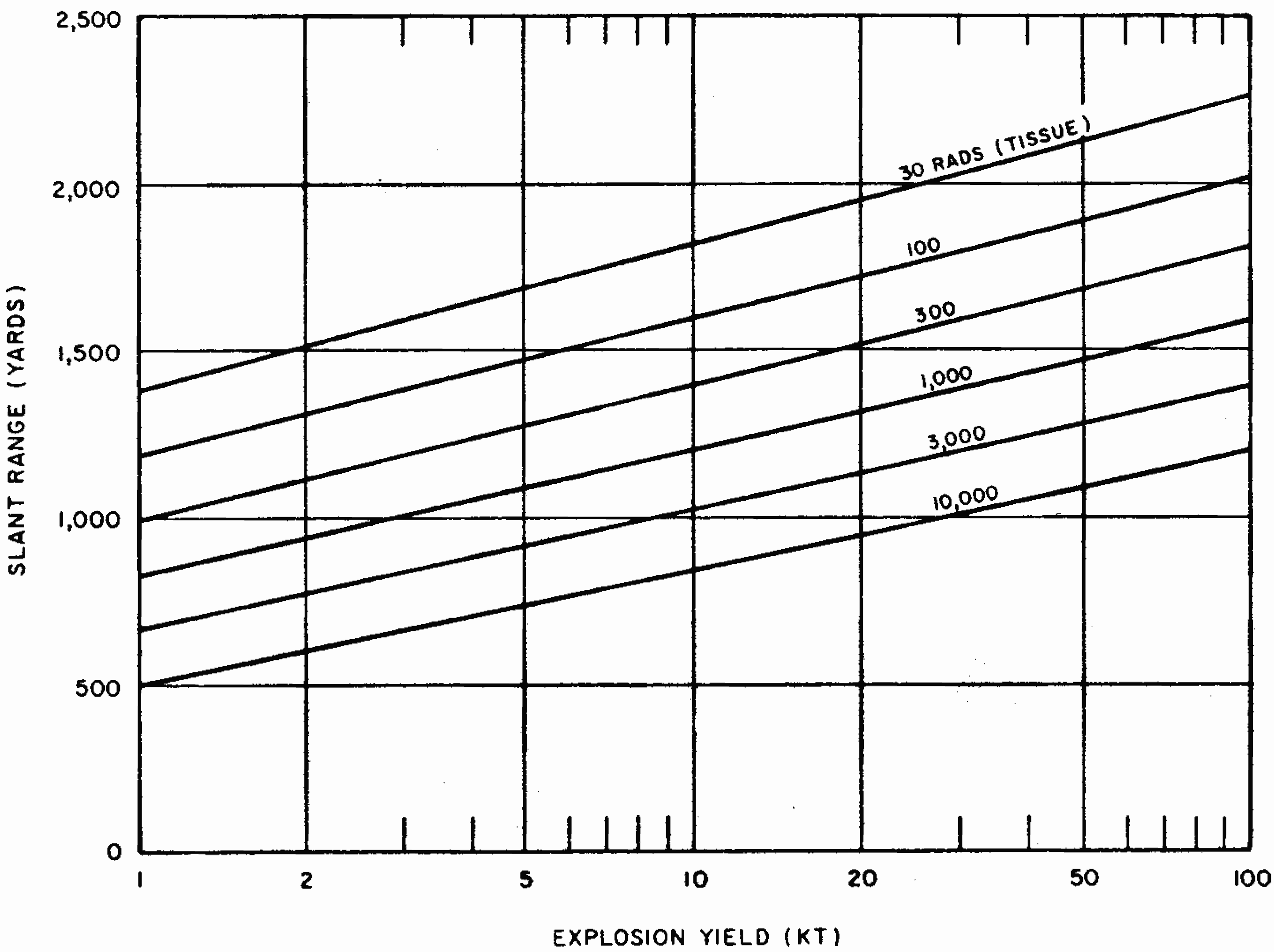
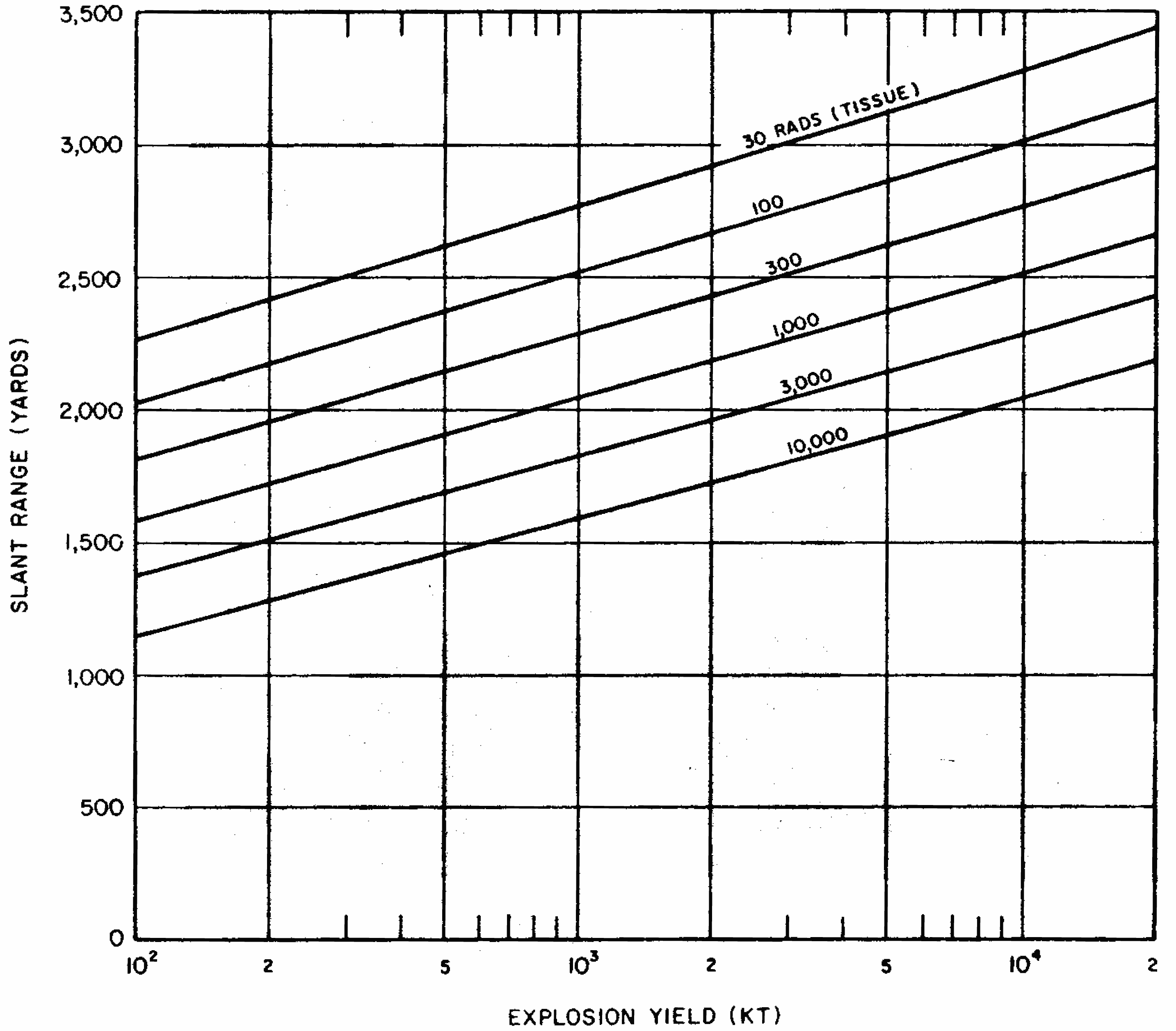
8.26 Indirect effects of nuclear radiations, notably chemical changes, have also been used for measurement purposes. One example is the blackening (or fogging) of photographic film which appears after it is developed. Film badges for the measurement of nuclear radiations generally contain two or three pieces of film, similar to those used by dentists for taking X rays. They are wrapped in paper (or other thin material) which is opaque to light but is readily penetrated by gamma rays. The films are developed and the degree of fogging observed is a measure of the gamma-ray exposure.
8.27 Other optical density dosimeters depend on the production by radiation of stable color centers which absorb light at a certain wavelength. An example is a device that measures radiation by a change in the transmission of light through a cobalt-glass chip. A lead borate glass containing bismuth has also been developed for the measurement of high levels of radiation, specifically for use in mixed gamma-neutron environments. Other materials that are utilized in instruments for the measurement of radiation by color changes include dyed plastics, such as blue cellophane and “cinemoid” film, i.e., a celluloid-like film containing a red dye.
8.28 In practice, measuring instruments do not determine the exposure in roentgens or the absorbed dose in rads directly. One or other of several observable effects, such as current pulses produced by ionization, scintillations, changes in optical response, or temperature rise, serves as the basis for the actual determination. The instruments can indicate the exposure in roentgens or the dose in rads after being calibrated with a standard gamma-ray source, usually a known quantity of a radioactive material that emits a gamma ray of the appropriate energy at a known rate.
8.29 Some instruments can record both the total radiation dose (or exposure) and the dose (or exposure) rate, but most radiation measuring devices are designed to indicate either the total or the rate. Total radiation doses (or exposures) are measured by personnel dosimeters worn by individuals who may be exposed to unusual amounts of nuclear radiation in the course of their work. Examples of such instruments are pocket ion chambers, optical density devices (especially film badges). and photoluminescent, thermoluminescent, and color-change dosimeters. Calorie meters also measure total radiation doses. The charge collection time in semiconductor detectors is so short that these instruments lend themselves to the measurement of gamma-ray dose rates in pulses of very short duration as well as of the total dose.
8.30 Dose (or exposure) rates are usually determined by what are called “survey meters.” They may be ion chambers, Geiger-Mueller tubes, or scintillation detectors, together with associated electronic counting circuitry. In general, these survey meters are portable and battery powered. The dose-rate measurement may be converted into the total radiation dose by multiplying the properly averaged dose rate by the total time of exposure.
GAMMA-RAY DOSE DEPENDENCE ON YIELD AND DISTANCE
8.31 The biological effects of various gamma-radiation doses will be considered more fully in Chapter XII. However, in order to provide some indication of the significance of the numbers given below, it may be stated that a single absorbed dose of gamma rays of less than 25 rads (in body tissue) will produce no detectable clinical effects in humans. Larger doses have increasingly more serious consequences and whole-body doses of 1,000 rads would probably prove fatal in nearly all cases. although death would not occur until a few days later.
8.32 As is to be expected, the gamma-ray dose at a particular location, resulting from a nuclear explosion, is less the farther that location is from the point of burst. The relationship of the radiation dose to the distance is dependent upon two factors, analogous to those which apply to thermal radiation. There is, first, the general decrease due to the spread of the radiation over larger and larger areas as it travels away from the explosion center. As with thermal radiation (§ 7.07), the dose received is inversely proportional to the square of the distance from the burst point, so that it is said to be governed by the “inverse square” law. Second, there is an attenuation factor to allow for the decrease in intensity due to absorption and scattering of gamma rays by the intervening atmosphere.
8.33 The gamma-radiation doses at known distances from explosions of different energy yields have been measured at a number of nuclear weapons tests. Extensive computer calculations have also been performed of the transport of gamma rays through the air. These calculations have been correlated with measurements of the gamma-ray transport from known sources and with observations made at nuclear explosions. The results obtained for air bursts are summarized in the form of two graphs: the first (Fig. 8.33a) shows the relation between yield and slant range for various absorbed gamma-ray doses (in tissue near the body surface, see § 8.18) for fission weapons; the second (Fig. 8.33b) gives similar information for thermonuclear weapons with 50 percent of their yield from fission(§ 1.72). The data are based on an average density of the air in the transmission path between the burst point and the target of O.9 of the normal sea-level density.5 Because of variations in weapon design and for other reasons (§ 8.127), the gamma-ray doses calculated from Figs. 8.33a and b are not exact for all situations that may arise. Figure 8.33a is considered to be reliable within a factor of 0.5 to 2 for most fission weapons, whereas the reliability factor for Fig. 8.33b is from 0.25 to 1.5 for most thermonuclear weapons. Interpolation may be used for doses other than those shown on the figures.
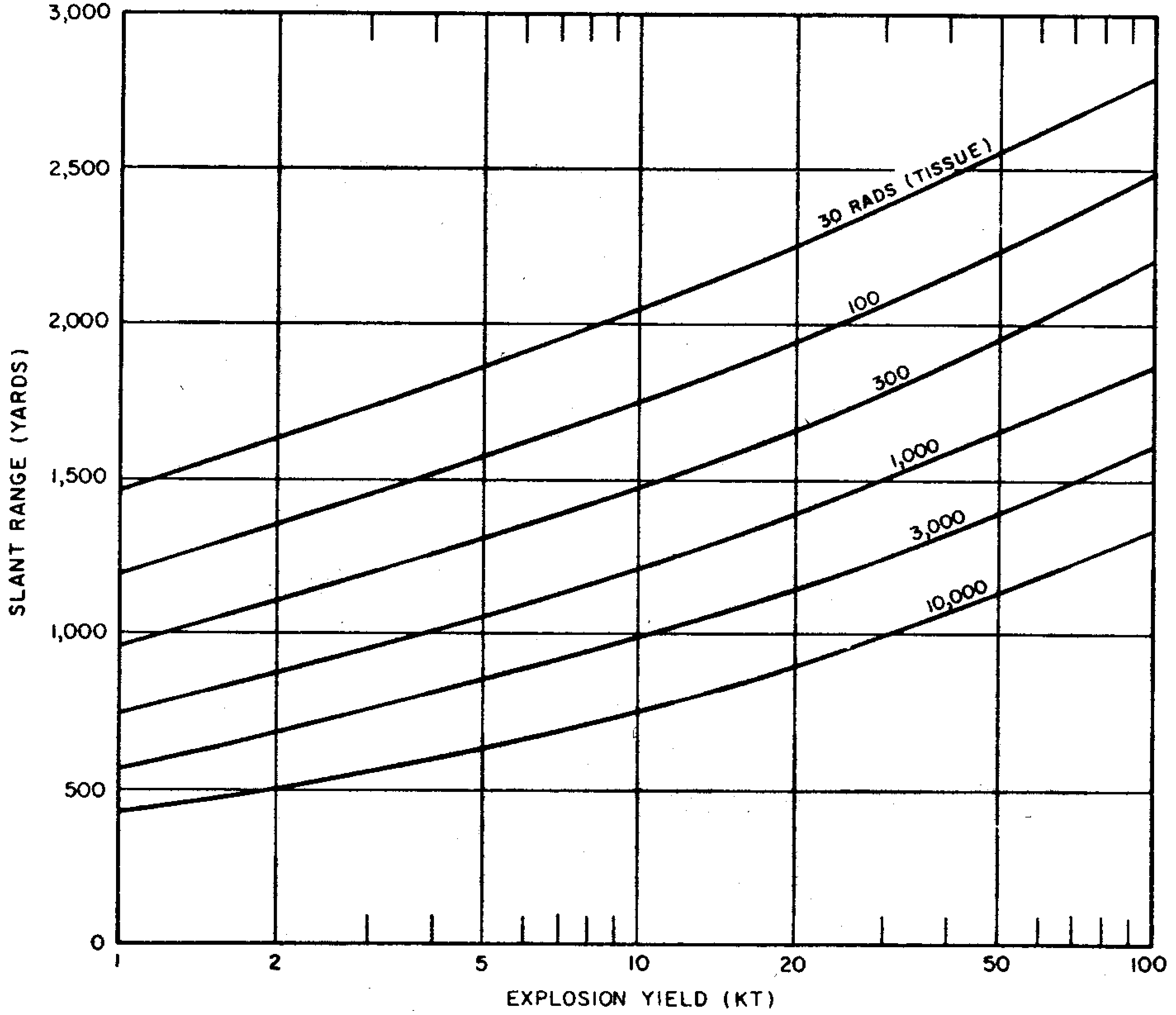
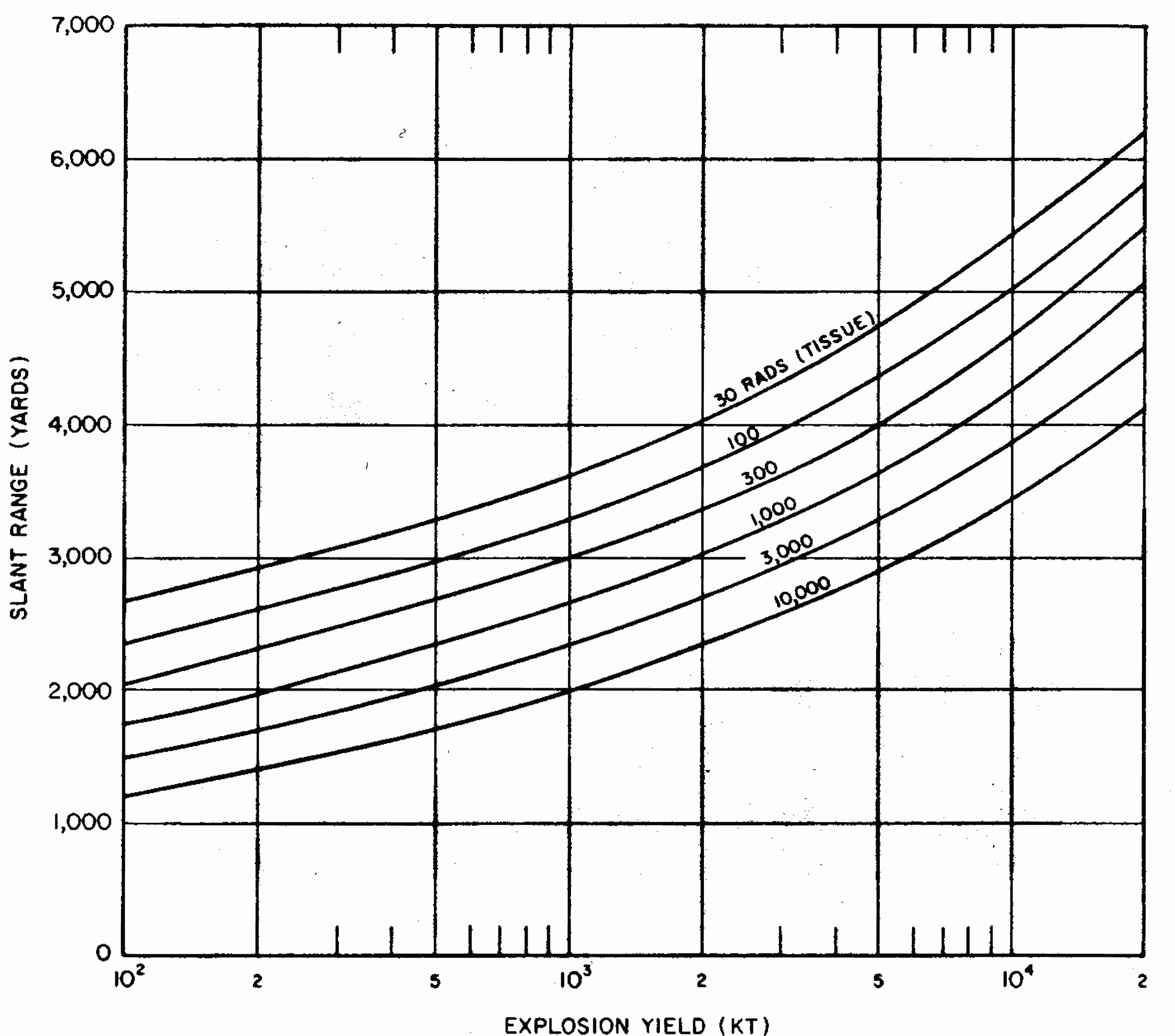
8.34 The use of the gamma-ray dose curves may be illustrated by determining the absorbed dose received at a distance of 2,000 yards from a 50-kiloton low air burst of a fission weapon. From Fig. 8.33a, the dose for the case specified is seen to be somewhat less than 300 rads. A reasonable interpolated value would appear to be about 250 rads.
8.35 The data in Figs. 8.33a and b are dependent upon the density of the air between the center of the explosion and the point on the ground at which the radiation is received. This is so because the air absorbs some of the gamma radiation in the course of its transmission; the dense air near the surface absorbs more than the less dense air at higher altitudes. If the actual average density is higher or lower than 0.9 of the normal sea-level value for which the curves were drawn, the gamma-ray dose will be decreased or increased, respectively.
8.36 It will be noted, especially in Fig. 8.33b, that for a specified dose, the slant range increases more rapidly in the higher explosion yield range, i.e., the slope of the curves becomes steeper. The cause is the sustained low air density following the passage of the positive phase of the shock wave (§ 3.04), particularly for explosions of high energy yield. The emission of gamma rays by the fission products is delayed (§ 8.13) and so these radiations do not reach distant points until the shock wave has passed and the air density has decreased. There is consequently less attenuation of the fission product gamma rays by the air than at lower energy yields. This effect is known as the “hydrodynamic enhancement” of the gamma-ray dose.
8.37 The foregoing figures were calculated for heights of burst of 200W0.4 feet and the conclusions are reasonably applicable provided the height of burst exceeds about 300 feet, even though the fireball may touch the earth’s surface. For a contact surface burst (§ 2.127 footnote) the dose for a specified explosion yield and range may be obtained upon multiplication of the corresponding dose in Fig. 8.33a or b by a factor which depends to some extent on both yield and range. The factors in Table 8.37 for some specific yields are averages which provide a fair approximation for distances of interest. The factors for intermediate yields may be obtained by interpolation. Interpolation between unity and the tabulated factor may also be used to obtain the appropriate factors for bursts between about 300 feet and the actual surface.
| Fig. 8.33a | Fig. 8.33b | ||
|---|---|---|---|
| Yield | Factor | Yield | Factor |
| 1 to 50 KT | ⅔ | 100 KT | 1 |
| 100 KT | 1 | 300 KT | 1¼ |
| 700 KT | 1½ | ||
| 2 MT | 2 | ||
| 5 to 20 MT | 3 | ||
SHIELDING AGAINST GAMMA RAYS
8.38 Gamma rays are absorbed (or attenuated) to some extent in the course of their passage through any material. As a rough rule, the decrease in the radiation intensity is dependent upon the mass (per unit area) of material that intervenes between the source of the rays and the point of observation. This means that it would require a greater thickness of a substance of low density, e.g., water, than one of high density, e.g., iron, to attenuate the radiations by a specified amount. Strictly speaking, it is not possible to absorb gamma rays completely. Nevertheless, if a sufficient thickness of matter is interposed between the radiation source, such as an exploding nuclear weapon, and an individual, the dose received can be reduced to negligible proportions.
8.39 The simplest case of gamma ray attenuation is that of a narrow beam of monoenergetic radiation, i.e., radiation having a single energy, passing through a relatively thin layer of shielding material. In these special (and hypothetical) circumstances, theoretical considerations lead to the concept of a “tenth-value” thickness as a measure of the effectiveness of the material in attenuating gamma rays of a given energy (cf. § 8.95 et seq.). A tenth-value thickness is defined as the thickness of the specified material which reduces the radiation dose (or dose rate) to one tenth of that falling upon it; in other words, one tenth-value thickness of the material would decrease the radiation by a factor of ten. Thus, if a person were in a location where the tissue dose is 500 rads, e.g., of initial gamma radiation, with no shielding, the introduction of the appropriate tenth-value thickness of any substance would decrease the dose to (approximately) 50 rads. The addition of a second tenth-value thickness would result in another decrease by a factor of ten, so that the dose received would be (approximately) 5 rads. Each succeeding tenth-value thickness would bring about a further reduction by a factor of ten. Thus, one tenth-value thickness decreases the radiation dose by a factor of (approximately) 10; two tenth-value thicknesses by a factor of 10 × 10, i.e., 100; three tenth-value thicknesses by a factor of 10 × 10 × 10, i.e., 1,000; and so on.6
8.40 In shielding against gamma radiations from a nuclear explosion the conditions leading to the tenth-value thickness concept do not exist. In the first place, the gamma-ray energies cover a wide range, the radiations are spread over a large area, and thick shields are necessary in regions of interest. Evaluation of the effectiveness of a given shield material is then a complex problem, but calculations have been made with the aid of electronic computers. It has been found that, beyond the first few inches of a shielding material, the radiation attenuation can be expressed with fair accuracy in many cases in terms of an effective tenth-value thickness. This useful result apparently arises from the fortuitous cancellation of factors which have opposing effects on the simple situation considered in § 8.39. In the first few inches of the shield the attenuation is generally greater than indicated by the effective tenth-value thickness and so use of the latter would be conservative.
8.41 The effective tenth-value thicknesses of some materials of interest in radiation shielding are given in Table 8.417 for broad beams of gamma rays emitted by the fission products in the first minute after the detonation and for those (secondary gamma rays) accompanying the capture of neutrons by nitrogen in the air (§ 8.11). These particular radiations were chosen because they are representative of the main constituents of the initial gamma rays. The thickness of any material required to decrease the nitrogen capture (secondary) gamma rays to one-tenth is about 50 percent greater than for the fission product gamma rays; this is because the former have a considerably higher energy.
| Fission Product | Nitrogen Capture | ||||
|---|---|---|---|---|---|
| Material | Density (lb/cu ft) | Tenth-Value Thickness (inches) | D × T (lb/sq ft) | Tenth-Value Thickness (inches) | D × T (lb/sq ft) |
| Steel (Iron) | 490 | 3.3 | 135 | 4.3 | 176 |
| Concrete | 146 | 11 | 134 | 16 | 194 |
| Earth | 100 | 16 | 133 | 24 | 200 |
| Water | 62.4 | 24 | 125 | 39 | 201 |
| Wood | 40 | 38 | 127 | 63 | 210 |
8.42 The second column for each type of gamma radiation, designated D x T (lb/sq ft), gives the product of the density, D, of the material (in lb/cu ft) and the tenth-value thickness, T (in feet). It will be noted that D x T is roughly constant for a given gamma radiation. This is the basis of the statement in § 8.38 that gamma-ray attenuation is determined approximately by the mass (per unit area) of the shielding material. If the tenth-value thickness for a particular material is not known, but the density is, a fair estimate can be made by assuming D x T to be 130 lb/sq ft for fission product gamma rays and 200 lb/sq ft for nitrogen capture gamma rays. To determine the effectiveness of a given shield as a protection against the initial radiation from a nuclear explosion, it is recommended that the higher of these values be employed. The result will indicate a smaller degree of protection than can actually be obtained, but it is better to be conservative in this respect than to overestimate the effectiveness of the shield.
8.43 A more accurate estimate of the protection that can be provided by a particular shield between the source of the radiation and the target, e.g., a person, can be made by taking a number of factors into consideration. These include the energy distribution of the gamma radiation falling on the shield, the angle of incidence of the radiation, and the geometry (or form) of the shielding material. Such considerations make it necessary to use computer methods to calculate the shielding provided by even simple structures. Estimates of the effectiveness of some common shelters in shielding from initial gamma radiation (and neutrons) are given in Table 8.72. (Data for these same structures for residual (fallout) gamma rays will be found in Table 9.120.)
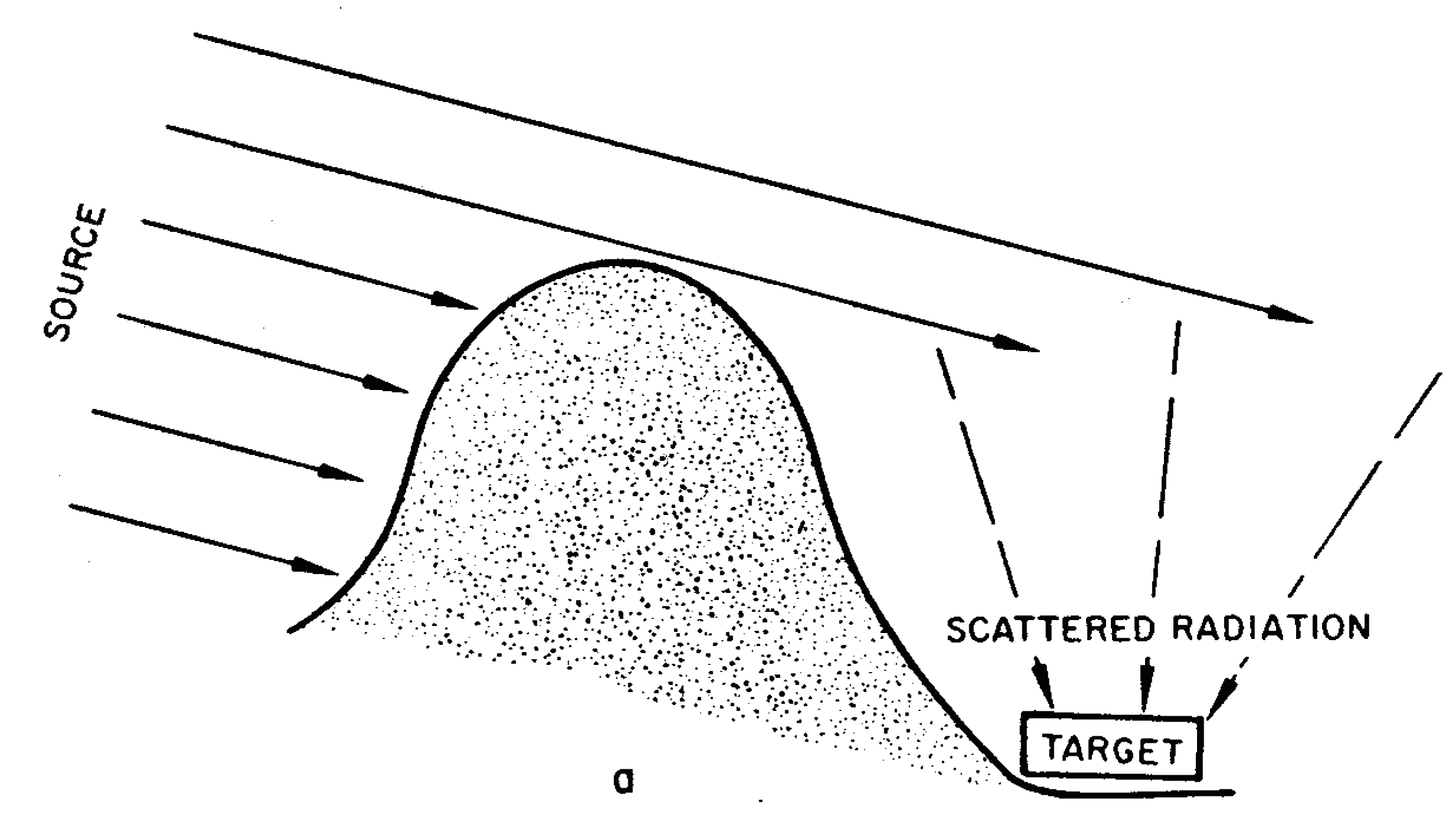
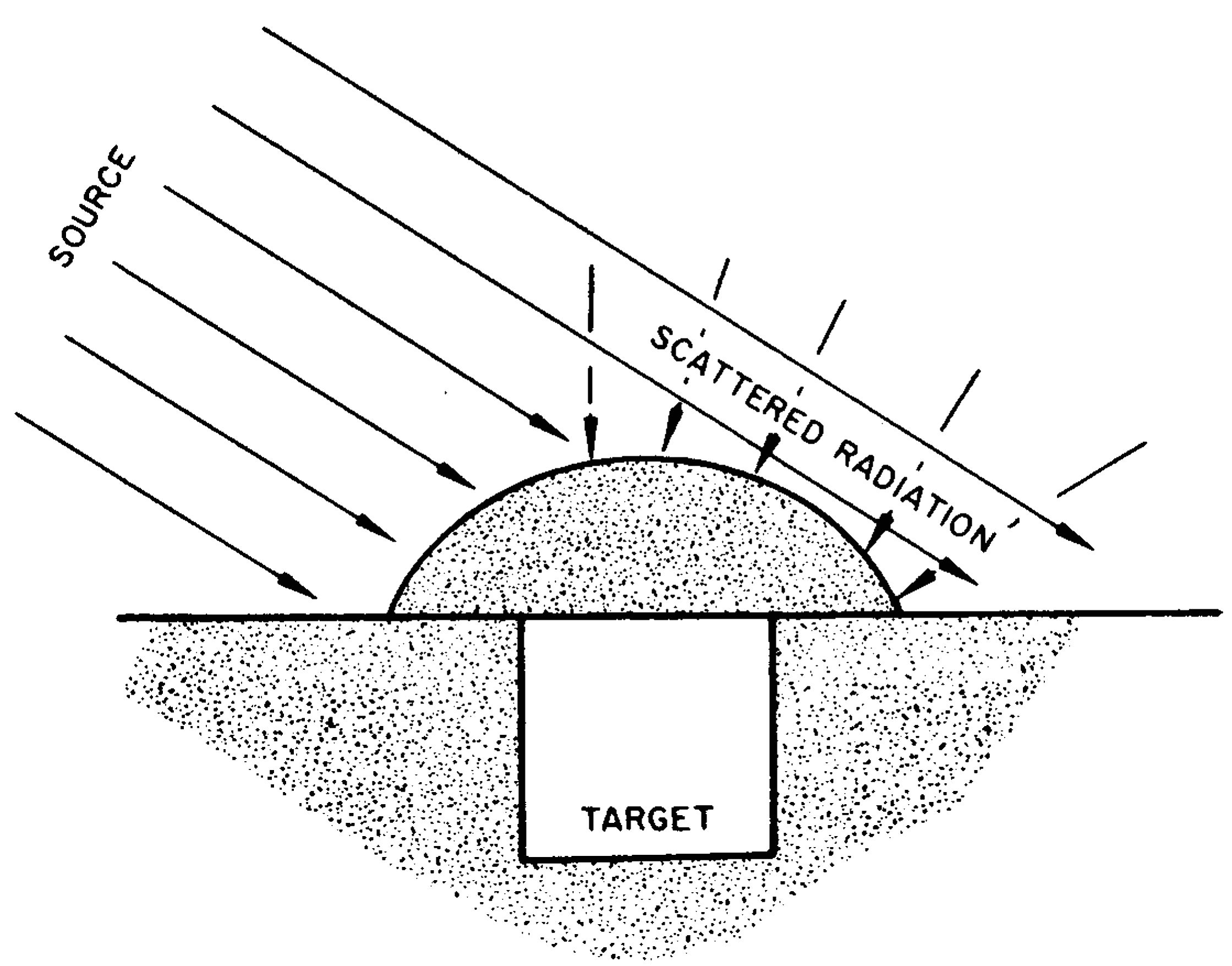
8.44 In a vacuum, gamma rays travel in straight lines with the speed of light. However, in its passage through the atmosphere, gamma radiation, like thermal radiation, is scattered, especially by the oxygen and nitrogen in the air. Consequently, gamma rays will reach a particular target on the ground from many directions. Most of the dose received will come from the direction of the explosion, but a considerable amount of radiation will arrive from other directions. The gamma radiation reaching a target as a result of scattering in the air is called “skyshine.”
8.45 The fact that gamma rays can reach a target from directions other than that of the burst point has an important bearing on the problem of shielding. A person taking shelter behind a single wall, an embankment, or a hill will be shielded, to some extent, from the direct gamma rays, but will still be exposed to the scattered radiation (or skyshine), as shown by the broken lines in Fig. 8.45a. Adequate protection from gamma rays can be secured only if the shelter is one which surrounds the individual, so that he can be shielded from all directions (Fig. 8.45b). In this case, both direct and scattered radiations can be attenuated. The variation in the amounts of radiation received at a target from different directions is called the “angular distribution.” It has been found that the angular distribution of the initial gamma radiation is relatively insensitive to the type of weapon and to the distance of the target from the explosion point.
RATE OF DELIVERY OF INITIAL GAMMA RAYS
8.46 Radiation dose calculations based on Figs. 8.33a and b involve the assumption that the exposure lasts for the whole minute which was somewhat arbitrarily set as the period in which the initial nuclear radiation is emitted. It is important to know, however, something about the rate at which the radiation is delivered from the exploding weapon. If this information is available, it is possible to obtain some idea of the dose that would be received if part of the radiation could be avoided, e.g., by taking shelter within a second or two of observing the luminous flash of the explosion.
8.47 The rate at which gamma-ray energy is released from a weapon is shown in Fig. 8.14. But the rate at which this energy is received at a distant target depends upon a number of factors; the most significant are the energy yield of the explosion and the distance from the burst point. These two quantities affect the relative importance of the several components of the initial gamma radiation. The larger the yield and the greater the distance, the greater will be the hydrodynamic enhancement of the fission product gamma rays(§ 8.36). As this enhancement is increased, the relative importance of the fission product gamma rays is increased. Thus, for larger yields and greater distances, the fission product gamma rays, which are important at late times relative to the other components of the initial gamma radiation, provide a larger percentage of the total dose. The percentage of the total dose received up to various times for two different cases is shown in Fig. 8.47. One curve refers to a distance of 1,000 yards from a 20-kiloton air burst and the other to 2,500 yards from a 5-megaton explosion. It is seen that in the former case about 65 percent and in the latter case about 5 percent of the total initial gamma radiation dose is received during the first second after the detonation.
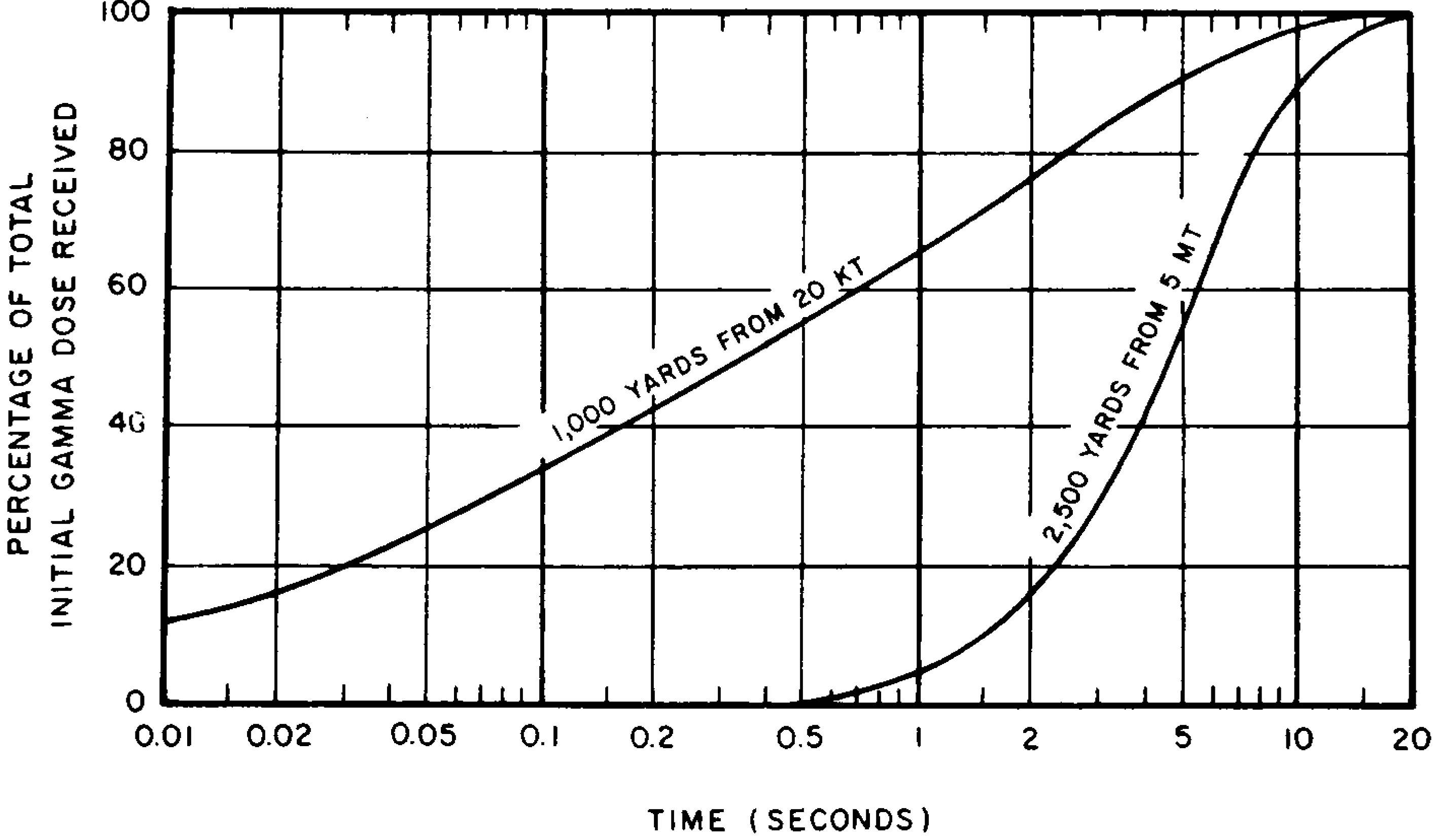
8.48 If some shelter could be obtained, e.g., by falling prone behind a substantial object, within a second of seeing the explosion flash, in certain circumstances it might make the difference between life and death. The curves in Fig. 8.47 show that avoidance of part of the initial gamma-ray dose would be more practicable for explosions of higher energy yields.
NEUTRONS
SOURCES OF NEUTRONS
8.49Although neutrons are nuclear particles of appreciable mass, whereas gamma rays are electromagnetic waves (§ 8.17), their harmful effects on the body and their ability to damage certain materials are similar in character. Like gamma rays, only very large doses of neutrons may possibly be detected by the human senses. Neutrons can penetrate a considerable distance through the air and constitute a hazard that is greater than might be expected from the small fraction (about 1 percent) of the explosion energy which they carry.
8.50 Essentially all the neutrons accompanying a nuclear explosion are released either in the fission or fusion process(§§ 1.42, 1.69). All of the neutrons from the latter source and over 99 percent of the fission neutrons are produced almost immediately, within less than a millionth of a second of the initiation of the explosion. These are referred to as the “prompt” neutrons. In addition, somewhat less than 1 percent of the fission neutrons, called the “delayed” neutrons, are emitted subsequently. The majority of these delayed neutrons are released within the first minute, and so constitute part of the initial nuclear radiation. At distances greater than about 2,000 yards from a multimegaton explosion, the dose from delayed neutrons can exceed that from prompt neutrons, because the delayed neutrons are subject to hydrodynamic enhancement (§ 8.36) whereas the prompt neutrons are not. Both doses are, however, much less than the gamma-ray dose for high-yield weapons. Neutrons are also produced by the action of high-energy gamma rays on the weapon materials, but their contribution is minor.
8.51 Despite their almost instantaneous release, the prompt fission neutrons are slightly delayed in escaping from the environment of the exploding weapon. This delay arises from the numerous scattering collisions suffered by the neutrons with the nuclei present in the weapon residues. As a result, the neutrons traverse a complex zigzag path before they finally emerge. However, they move so fast that the delay in the escape of the prompt neutrons is much less than a one-thousandth part of a second. At distances from the burst where they represent a hazard, nearly all of the neutrons are received within a second of the explosion, that is, before the arrival of the fission product gamma rays. The evasive action described in § 8.48 for gamma rays thus has little effect on the neutron dose received.
8.52 The neutrons produced in the fission process have a range of energies, but they are virtually all in the region of high energy. Such high-energy neutrons are the fast neutrons referred to in § 8.09, their energy being kinetic in nature, i.e., energy of motion. In the course of scattering collisions with atomic nuclei, there is an exchange of energy between the fast neutrons and the nuclei. Within the weapon itself, where heavy nuclei, e.g., of uranium, are present, some of the neutrons lose energy as a result of inelastic scattering, the energy removed being emitted in the form of gamma radiation (§ 8.09). In other collisions, especially with light nuclei, there is a simple transfer of kinetic energy from the fast neutron to the struck nucleus; these are “elastic collisions” and are not accompanied by gamma radiation. Because of the variety of collisions which occur with different nuclei, the neutrons leaving the region of the explosion have speeds (or energies) covering a wide range, from fast through intermediate to slow. The neutrons of lowest energy (or speed) are often called “thermal” neutrons because they are approximately in thermal (or temperature) equilibrium with their surroundings.
8.53 As a consequence of the various interactions described above, the neutrons that emerge from the region of the explosion have a very different energy distribution, i.e., “neutron energy spectrum,” than when they were formed in the fission and fusion reactions. Furthermore, the energy spectrum may change as the neutrons travel through the air. For example, the neutrons leaving the weapon environment undergo scattering collisions with nuclei of nitrogen, oxygen, and other elements in the atmosphere. These collisions are less frequent than within the weapon because of the lower density and smaller concentration of nuclei. Nevertheless, the results of the collisions are important. In the first place, the fractional decrease in neutron energy per elastic scattering collision is, on the average, greatest for light nuclei. The nuclei of oxygen and nitrogen are relatively light, so that the neutrons are appreciably slowed down by elastic scattering collisions in the air. Some of the collisions with nitrogen result in inelastic scattering which removes energy from the neutrons and is a substantial source of gamma radiation (§ 8.09, Fig. 8.14). Inelastic scattering of high-energy neutrons by oxygen also results in energy removal and provides a less important source of gamma radiation (§ 8.107).
8.54 In some collisions, particularly with nitrogen nuclei, the neutrons can be captured (§ 8.11), so that they are completely removed. The probability of capture is greatest with the slow (low-energy) neutrons. Consequently, in their passage through the air, from the weapon to a location on the ground, for example, there are many interactions involving the neutrons. There is a tendency for the fast (high-energy) neutrons to lose some of their energy and to be slowed down. At the same time, the slower neutrons have a greater chance of being captured and eliminated, as such, from the nuclear radiation, although the capture usually leads to the emission of gamma rays.
8.55 It is important in connection with the measurement of nuclear weapon neutrons and the study of their biological effects to know something of the neutron energy spectrum and its variation with distance from the explosion. From measurements made during nuclear tests in the field, measurements with laboratory calibrated sources, and extensive computer calculations, it appears that the neutron energy spectrum for fission weapons remains essentially the same for a given weapon over the range of distances that are of biological interest. This condition is referred to as an “equilibrium spectrum.”
8.56 The occurrence of an equilibrium spectrum is related to a combination of circumstances which arise during passage of the neutrons through the air; the loss of the slower neutrons by capture, e.g., by nitrogen nuclei, is compensated by the slowing down of fast neutrons. Consequently, the proportion (or fraction) of neutrons present in any particular energy range appears to be essentially constant at all distances of interest. The total number of neutrons received per unit area, however, at a given location is less the farther that point is from the explosion, because, in addition to being spread over a large area (cf. § 8.32), some of the neutrons are removed by capture.
8.57 The thermonuclear reaction between deuterium and tritium results in the liberation of neutrons with energies of 14.1 MeV. This energy is considerably greater than that of essentially all the fission neutrons and is also much greater than the energy of the neutrons produced by the other thermonuclear reactions (§ 1.69). These neutrons of very high energy undergo reactions within the exploding weapon similar to those described in § 8.52. Consequently some of the high-energy neutrons are emitted from the region of the explosion with energies lower than 14.1 MeV. Nevertheless, sufficient quantities of energetic neutrons emerge from a thermonuclear weapon to cause a peak in the neutron spectrum at energies in the range of 12 to 14 MeV. This peak is in contrast to the continuous decrease in the number of neutrons with increasing neutron energy observed for fission weapons. The existence of the high-energy peak in the neutron energy spectrum from thermonuclear weapons prevents the occurrence of an equilibrium spectrum until the neutrons have traveled long distances in air (§ 8.117 et seq.).
MEASUREMENT OF NEUTRON FLUX
8.58 Neutrons, being electrically neutral particles, do not produce ionization or excitation directly in their pas sage through matter. They can, however, cause these effects indirectly as a result of their interaction with certain light nuclei. When a fast neutron collides with the nucleus of a hydrogen atom, for example, the neutron may transfer a large part of its energy to that nucleus. As a result, the hydrogen nucleus is freed from its associated electron and moves off as a high-energy proton. Such a proton is capable of producing a considerable number of ion pairs in its passage through a gas or it can cause electronic excitation. Thus, the interaction of a fast neutron with hydrogen (or with any substance containing hydrogen) can cause ionization or excitation to occur indirectly.8 The interaction of neutrons with hydrogen thus makes it possible to use both ionization and scintillation counters as neutron detectors. For example, if a hydrogenous material is impregnated with a substance that is capable of producing scintillations, protons released by neutrons interacting with hydrogen atoms cause the excitation of the scintillation material.
8.59 Neutrons in the slow and moderate speed ranges can produce ionization and excitation indirectly in other ways. When such neutrons are captured by the lighter isotope of boron (boron-10), two electrically charged particles-a helium nucleus (alpha particle) and a lithium nucleus-of high energy are formed. Neutrons also can be captured in the lighter isotope of lithium (lithium-6) to produce a tritium nucleus and an alpha particle (§ 1.70), or the neutrons can be captured by nitrogen nuclei and high-energy particles are emitted (§ 8.110). In each of these reactions, the resulting charged particles can produce ion pairs or excitation. In direct ionization by neutrons can also result from the fission of plutonium or uranium isotopes. The fission fragments are electrically charged particles (ions) of high energy which leave considerable ionization in their paths.
8.60 All of the foregoing indirect ionization or excitation processes can be used to detect and measure neutron intensities. The quantity determined, either directly or indirectly, is called the “neutron flux”; it is the product of the neutron density, i.e., the number per unit volume, and the average velocity. The instruments employed for the measurement of neutron flux, such as boron counters and fission chambers, are somewhat similar, in general principle, to the dose rate (survey) meters commonly used for gamma radiations (§ 8.30). “Tissue equivalent” chambers have been developed in which the ionization produced indirectly by neutrons is related to the energy which would be taken up from these neutrons by animal tissue. Thus, the absorbed dose in rads (tissue) can be determined in this manner.
8.61 In addition to the procedures described above, “foil activation” methods have been extensively used in the detection and measurement of neutrons in various energy ranges. These methods are based upon the fact that certain elements become radioactive as a result of the capture of neutrons (§ 8.16). Under appropriate conditions, the extent of the radioactivity, as measured by the rate of emission of radiation (beta or gamma or both), is related to the “integrated flux,” or “fluence,” of incident neutrons, i.e., the product of the flux and time, expressed as neutrons per square centimeter (neutrons/cm2). Hence, by the use of appropriate conversion factors, neutron fluence can be calculated.9 In practice the elements are used in the form of thin sheet or foil, so that they produce a minimum disturbance of the neutron field. The technique is referred to as “activation detection” and the materials employed are known as “activation detectors.” An activation detector which has an appreciable probability of reaction only when the energy of the neutron exceeds a particular (threshold) value is called a “threshold detector.” The procedure is then described as the “threshold detector technique” and is used to determine the number of neutrons with energies in excess of the threshold value.
8.62 The “fission foil” method, as its name implies, makes use of fission reactions. A thin layer of a fissionable material, such as an isotope of uranium or plutonium, is exposed to neutrons. The fission products formed are highly radioactive, emitting beta particles and gamma rays. By measuring the radioactivity produced in this manner, the amount of fission and, hence, the neutron fluence to which the fissionable material was exposed can be determined.
NEUTRON DOSE DEPENDENCE ON YIELD AND DISTANCE
8.63 A basic difficulty in expressing the relation between the neutron dose, yield, and the distance from a nuclear explosion is the fact that the results vary significantly with changes in the characteristics of the weapon. The materials, for example, have a considerable influence on the extent of neutron capture and, consequently, on the number and energy distribution of the fission neutrons that succeed in escaping into the air. Further, the thermonuclear reaction between deuterium and tritium is accompanied by the liberation of neutrons of high energy (§ 8.57). Hence, it is to be expected that, for an explosion in which part of the energy yield arises from thermonuclear (fusion) processes, there will be a larger proportion of high-energy (fast) neutrons than from a purely fission explosion.
8.64 In view of these considerations, it is evident that the actual number of neutrons emitted per kiloton of ex plosion energy yield, as well as their energy distribution, may differ not only for weapons of different types, i.e., fission and fusion, but also for weapons of the same kind. Hence, any curve which purports to indicate the variation of neutron dose with yield and distance cannot be correct for all situations that might arise. It is with this limitation in mind that the curves in Figs. 8.64a and bare presented; the former is for fission weapons and the latter for thermonuclear weapons with 50 percent of their yield from fission. The estimated reliability factors are the same as given in § 8.33 for Figs 8.33a and b, respectively. The curves give absorbed neutron doses in tissue close to the surface of the body received near the ground for low air bursts. The data are based on an average air density in the transmission path of 0.9 of the normal sea-level density. If the actual average air density is higher or lower than this, the neutron dose will be decreased or increased, respectively.
8.65 When comparing or combining neutron doses with those from gamma rays (Figs. 8.33a and b), it should be noted that the biological effects of a certain number of rads of neutrons are often greater than for the same number of rads of gamma rays absorbed in a given tissue(§ 12.97). As for gamma rays, the neutron dose decreases with distance from the explosion as a result of the inverse square law and attenuation by absorption and scattering in the atmosphere. However, since the prompt neutrons are emitted during a short time (§ 8.51), and since those of major biological significance travel much faster than the blast wave, there is no hydrodynamic enhancement of the (prompt) neutrons dose as there is for fission product gamma rays. This is one reason why the gamma-ray dose increases more rapidly with the energy yield than does the neutron dose. The data in Figs. 8.64a and b may be regarded as applying to air bursts. For contact surface bursts, the prompt neutron dose may be taken as one-half the value for a corresponding air burst. For heights of burst below 300 feet, the dose may be estimated by interpolation between the values for an air burst and a contact surface burst.
SHIELDING AGAINST NEUTRONS
8.66 Neutron shielding is a different, and more difficult, problem than shielding against gamma rays. As far as the latter are concerned, it is merely a matter of interposing a sufficient mass of material between the source of gamma radiation and the recipient. Heavy metals, such as iron and lead, make good gamma-ray shields because of their high density. These elements alone, however, are not quite as satisfactory for neutron shielding. An iron shield will attenuate weapon neutrons to some extent, but it is less effective than some of the types described below.
8.67 The attenuation of neutrons from a nuclear explosion involves several different phenomena. First, the very fast neutrons must be slowed down into the moderately fast range; this requires a suitable (inelastic) scattering material, such as one containing barium or iron. Then, the moderately fast neutrons have to be decelerated (by elastic scattering) into the slow range by means of an element of low atomic weight (or mass number). Water is very satisfactory in this respect, since its two constituent elements, i.e., hydrogen and oxygen, both have low atomic weights. The slow (thermal) neutrons must then be absorbed. This is not a difficult matter, since the hydrogen in water will serve the purpose. However, neutron inelastic scattering reactions and most neutron capture reactions are accompanied by the emission of gamma rays (§§ 8.53, 8.54). Consequently, sufficient gamma attenuating material must be included to minimize the escape of the gamma rays from the shield.
8.68 In general, concrete or damp earth would represent a fair compromise for neutrons, as well as for gamma-ray shielding. Although these materials do not normally contain elements of high atomic weight, they do have a fairly large proportion of hydrogen to slow down and capture neutrons, as well as calcium, silicon, and oxygen to absorb the gamma radiations. A thickness of 12 inches of concrete, for example, will decrease the neutron fluence from a thermonuclear weapon by a factor of about 10, and 24 inches by a factor of roughly 100. The high energy initial gamma radiation would be decreased to a somewhat lesser extent (see Table 8.41), but, in sufficient thickness, concrete could be used to provide shielding against both neutrons and gamma rays from a nuclear explosion. Damp earth may be expected to act in a similar manner, although about 50 percent greater thickness would be required.
8.69 An increase in the absorption of the nuclear radiations can be achieved by using a modified (”heavy”) concrete made by adding a considerable proportion of an iron (oxide) ore, e.g., limonite, to the mix and incorporating small pieces of iron, such as steel punchings. Alternatively, the mineral barytes, which is a compound of barium, may be included in the concrete. The presence of a heavy element improves both the neutron and gamma-ray shielding properties of a given thickness (or volume) of the material. Attenuation of the neutron fluence from a thermonuclear weapon by a factor of 10 requires about 7 inches of this heavy concrete.
8.70 The presence of boron or a boron compound in neutron shields has certain advantages. The lighter (boron-10) isotope of the element captures slow neutrons very readily (§ 8.59), the process being accompanied by the emission of gamma rays of moderate energy (0.48 MeV) that are not difficult to attenuate. Thus, the mineral colemanite, which contains a large proportion of boron, can be incorporated into concrete in order to improve its ability to absorb neutrons.
8.71 It was pointed out in § 8.45 that, because of the scattering experienced by gamma rays, an adequate shield must provide protection from all directions. Somewhat the same situation applies to neutrons. As seen earlier, neutrons undergo extensive scattering in the air, so that, by the time they reach the ground, even at a moderate distance from the explosion, their directions of motion are almost randomly distributed. Partial protection from injury by neutrons may be obtained by means of an object or structure that provides shielding only from the direction of the explosion, although better protection, as in the case of gamma rays, would be given by a shelter which shields in all directions.
8.72 In addition to the complexities introduced by the arrival of neutrons at a target from many directions, the distribution in energy from each direction makes it impractical to calculate the shielding effectiveness of even simple structures without resort to complex computer codes. Estimates of the shielding afforded by various structures are given in Table 8.72 in terms of a “dose transmission factor”; this is defined as the ratio of the dose received behind the shield to the dose at the same location in the absence of shielding. Some of the transmission factors were obtained by measurements at weapons tests or are extrapolations from such measurements. Others were obtained by relatively detailed calculations, whereas still others are mere estimates. Ranges of values are given for the dose transmission factors for two reasons: uncertainties in the estimates themselves and variations in the degree of shielding that may be obtained at different locations within a structure.
| Structure | Initial Gamma Rays | Neutrons |
|---|---|---|
| Three feet underground | 0.002-0.004 | 0.002-0.01 |
| Frame House | 0.8-1.0 | 0.3-0.8 |
| Basement | 0.1-0.6 | 0.1-0.8 |
| Multistory building (apartment type): | ||
| Upper stories | 0.8-0.9 | 0.9-1.0 |
| Lower stories | 0.3-0.6 | 0.3-0.8 |
| Concrete blockhouse shelter: | ||
| 9-in. walls | 0.1-0.2 | 0.3-0.5 |
| 12-in walls | 0.05-0.1 | 0.2-0.4 |
| 24-in walls | 0.007-0.02 | 0.1-0.2 |
| Shelter, partly above grade: | ||
| With 2 ft earth cover | 0.03-0.07 | 0.02-0.08 |
| With 3 ft earth cover | 0.007-0.02 | 0.01-0.05 |
TRANSIENT-RADIATION EFFECTS ON ELECTRONICS (TREE)
GENERAL CHARACTERISTICS OF TREE
8.73The initial nuclear radiation, specifically gamma rays and neutrons, can affect materials, such as those used in electronics systems, e.g., radio and radar sets, gyroscopes, inertial guidance devices, computers, etc. The response of such systems to radiation from a nuclear explosion depends on the nature of the radiation absorbed and also on the specific component and often on the operating state of the system. The actual effects are determined by the characteristics of the circuits contained in the electronics package, the exact components present in the circuits, and the specific construction techniques and materials used in making the components.
8.74 The name commonly applied to the class of effects under consideration is “transient-radiation effects on electronics,” commonly abbreviated to the acronym TREE. In general, TREE means those effects occurring in an electronics system as a result of exposure to the transient initial radiation from a nuclear weapon explosion. The adjective “transient” applies to the radiation since it persists for a short time, i.e., less than 1 minute. The response, however, is not necessarily transient. In order to study the effects of nuclear radiations on electronics systems and components, the transient radiation from a weapon is simulated in the laboratory by means of controlled sources of both steady-state and transient radiations.
8.75 The term “electronics” as used in TREE may refer to any or all of the following: individual electronic component parts, component parts assembled into a circuit, and circuits combined to form a complete system. TREE studies may also include electro mechanical components connected to the electronics, e.g., gyros, inertial instruments, etc. Purely mechanical or structural components are excluded since they are much less sensitive to radiation than are components or systems that depend on electrical currents (or voltages) for their operation.
8.76 Radiation effects on electronics may be temporary or more-or-less permanent. Even though the effects on a particular component, e.g., a transistor, may be temporary, these effects may result in permanent damage to some other part of a circuit. The component responses of short duration are usually the result of ionization caused by gamma radiation and are dependent upon the dose rate, e.g., in rads per second, rather than the dose. The more permanent effects are generally-but not always--due to the displacement of atoms in a crystal lattice by high-energy (fast) neutrons. In such cases the extent of damage is determined by the neutron fluence, expressed in neutrons/cm2 (§ 8.61). When a permanent effect is produced in an electronic component by gamma radiation, the important quantity usually is the dose in rads. A brief description of the responses of some components of electronics systems are given below; the mechanisms of the interactions with nuclear radiations are explained later(§ 8.133 et seq.).
OBSERVED EFFECTS ON ELECTRONICS COMPONENTS
Solid-State Devices
8.77 Solid-state devices, such as diodes, transistors, and integrated circuits, are widely used in electronics systems. They consist of semiconductor materials that are quite sensitive to nuclear radiations. Temporary effects are the production of spurious current pulses caused by gamma rays absorbed in the solid. This phenomenon is turned to advantage in the semiconductor detectors of nuclear radiation (§ 8.22). The strength of the current pulse is proportional to the dose rate of the radiation and is much larger in a transistor than in a diode because the primary current resulting from ionization produces an amplified secondary current in the transistor.
8.78 Some of the changes caused by atomic displacements in a semiconductor disappear or “anneal” (§ 8.142) in a short time but others remain. Permanent changes in the physical properties of materials affect the operating characteristics of the diode or transistor. The latter are usually more sensitive to radiation and so the discussion here will be restricted to transistors. In most cases, d radiation in the current amplification (or gain) of transistors is the critical factor in determining the useful ness of electronic systems containing solid-state components.
8.79 There is a wide variation in the response of transistors to radiation, even among electronic devices designed to perform similar functions. The decrease in gain may become unacceptable at fast-neutron fluences as small as 1011 or as large as 1015 (or more) neutrons/cm2. (Fast-neutron fluences referred to in this section are fission neutrons with energies exceeding 10 keV, i.e., 0.01 MeV).10 The structure of the device has an important influence on the radiation resistance of a transistor. As a general rule, a thin base, as in high-frequency devices, and a small junction area favor radiation resistance. For example, diffuse-junction transistors are significantly more resistant than alloy-junction devices because of the smaller junction area. Junction and especially thin-film field-effect transistors can be made that are quite resistant to radiation. Certain types of the latter have remained operational after exposure to a fast-neutron fluence of 1015 neutrons/cm2.
8.80 Damage in MOS (metal-oxide semiconductor) field-effect transistors is caused primarily by gamma radiation rather than by neutrons; hence, the effects are reported in terms of the dose in rads (silicon). The most sensitive parameter to radiation in these devices is the threshold voltage, i.e., the value of the gate voltage for which current just starts to flow between the drain and the source. In general, gradual degradation, i.e., a shift of about 0.5 volt in the threshold voltage, begins at about 104 rads (silicon) and proceeds rapidly at higher doses. The sensitivity of MOS transistors to radiation is, however, dependent on the impurities in the gate oxide. With improvements in the technique for producing the oxide, the devices are expected to survive doses of 106 rads (silicon).
Vacuum Tubes and Thyratrons
8.81 The principal transient effect in vacuum tubes arises from the (Compton) electrons ejected by gamma rays (§ 8.89) from the structural parts of the tube into the evacuated region. These electrons are too energetic to be significantly influenced by the electric fields in the tube. However, their impact on the interior surfaces of the tube produces low-energy secondary electrons that can be affected by the existing electric fields, and as a result the operating characteristics of the tube can be altered temporarily. The grid is particularly sensitive to this phenomenon; if it suffers a net loss of electrons, its voltage will become more positive and there is a transient increase in the plate current. Large fluences of thermal neutrons, e.g., 1016 neutrons/cm2, can cause permanent damage to vacuum tubes as a consequence of mechanical failure of the glass envelope. But at distances from a nuclear explosion at which such fluences might be experienced, blast and fire damage would be dominant.
8.82 Gas-filled tubes (thyratrons) exposed to gamma radiation exhibit a transient, spurious firing due to partial ionization of the gas, usually xenon. Additional ionization is caused by collisions between ions and neutral molecules in the gas. As with vacuum tubes, large fluences of thermal neutrons can cause thyratrons to become useless as a result of breakage of the glass envelope or failure of glass-to-metal seals.
Capacitors, Resistors, and Batteries
8.83 Nuclear radiation affects the electrical properties of capacitors to some extent. Changes in the capacitance value, dissipation factor. and leakage resistance have been observed as a consequence of exposure. The effects are generally not considered to be severe for fast-neutron fluences less than 1015 neutrons/cm2. During a high-intensity pulse of nuclear radiation, the most pronounced effect in a capacitor is a transient change in the conductivity of the dielectric (insulating) material with a corresponding increase in the leakage currents through the capacitor.
8.84 Radiation effects in resistors are generally small compared with those in semiconductors and capacitors and are usually negligible. However, in circuits requiring high-precision carbon resistors transient effects may be significant at gamma-ray dose rates of 107 rads (carbon)/sec 11 and at fast-neutron fluences of 1014 neutrons/cm2. The transient effects are generally attributed to gamma rays that interact with materials to produce electrons; however, energetic neutrons can also cause significant ionization by recoiling nuclei. The transient effects on resistors include (1) a change in the effective resistance due to leakage in the insulating material and the surrounding medium, and (2) induced current that is the result of the difference between the emission and absorption of secondary electrons by the resistor materials. The permanent effects are generally due to the displacement of atoms by neutrons, thereby causing a change in the resistivity of the material.
8.85 Batteries are affected much less by radiation than other components. The effects of radiation on nickel-cadmium batteries appear to be insignificant at gamma-ray dose rates up to 107 rads (air)/sec. No radiation damage was apparent in a number of batteries and standard cells that were subjected to 1013> fast neutrons/cm2. Mercury batteries can withstand fast neutron fluences up to 1016 neutrons/cm2.
Cables and Wiring
8.86 It has been recognized for some time that intense pulses of radiation produce significant perturbation in electrical cables and wiring, including coaxial and triaxial signal cables. Even with no voltage applied to a cable, a signal is observed when the cable is exposed to a radiation pulse. The current associated with this signal is defined as a replacement current, since it is a current in an external circuit that is apparently necessary to replace electrons or other charged particles that are knocked out of their usual positions by the radiation. In addition there is a signal, attributed to what is called the conduction current, which varies with the voltage applied to the cable. It is ascribed to the conductivity induced in the insulating dielectric by the radiation. However, the conductivity current may also include substantial contributions from changes in the dielectric material. These can usually be identified by their gradual disappearance (saturation) after repeated exposures and by their reappearance after additional exposures in which there is a considerable change in the applied voltage, e.g., it is removed or reversed.
8.87 Nuclear radiation can have both temporary and permanent effects on the insulating material of cables. If ionization occurs in the material, the free electrons produced contribute to its conductivity. Hence, insulators are expected to have a temporary enhancement of conductivity in an ionizing radiation environment. Conduction in the insulator is frequently characterized by two components: (1) for very short radiation pulses, a prompt component whose magnitude is a function of only the instantaneous exposure rate, and (2) frequently at the end of the short radiation exposure, a delayed component having approximately exponential decay, i.e., rapid at first and then more and more slowly.
8.88 Permanent damage effects in cables and wiring are apparent as changes in the electrical properties of the insulating materials. When such damage becomes appreciable, e.g., when the resistance is reduced severely, electrical characteristics may be affected. The extent of the damage to insulating materials increases with the neutron fluence (or gamma-ray dose), humidity, and irradiation temperature. Certain types of insulation are quite susceptible to permanent damage. For example, silicon rubber is severely cracked and powdered by a fluence of 2 × 1015 fast neutrons/cm2. The approximate gamma-radiation damage thresholds for three common types of cable insulation are: polyethylene, 1 × 107 rads (carbon); Teflon TFE, 1 × 104 rads (carbon); and Teflon FEB, 2 × 106 rads (carbon). On the other hand, some irradiated polyolefins are capable of withstanding up to 5 × 109 rads (carbon). A considerable degree of recovery has been observed with respect to insulation resistance; this implies the possibility of adequate electrical serviceability after moderate physical damage.
TECHNICAL ASPECTS OF INITIAL NUCLEAR RADIATION12
INTERACTION OF GAMMA RAYS WITH MATTER
8.89 There are three important types of interaction of gamma rays with matter, as a result of which the photons (§ 1.74) are scattered or absorbed. The first of the these is called the “Compton effect.” In this interaction, the gamma ray (primary) photon collides with an electron and some of the energy of the photon is transferred to the electron. Another (secondary) photon, with less energy, then moves off in a new direction at an angle to the direction of motion of the primary photon. Consequently, Compton interaction results in a change of direction (or scattering) of the gamma-ray photon and a degradation in its energy. The electron which, after colliding with the primary photon, recoils in such a manner as to conserve energy and momentum is called a Compton (recoil) electron.
8.90 The total extent of Compton scattering per atom of the material with which the radiation interacts is proportional to the number of electrons in the atom, i.e., to the atomic number (§ 1.09). It is, consequently, greater per atom for an element of high atomic number than for one of low atomic number. The Compton scattering decreases with increasing energy of the gamma radiation for all materials, irrespective of the atomic number.
8.91 The second type of interaction of gamma rays and matter is by the “photoelectric effect.” A photon, with energy somewhat greater than the binding energy of an electron in an atom, transfers all its energy to the electron which is consequently ejected from the atom. Since the photon involved in the photoelectric effect loses all of its energy, it ceases to exist. In this respect, it differs from the Compton effect, in which a photon still remains after the interaction, although with decreased energy. The magnitude of the photoelectric effect per atom, like that of the Compton effect, increases with the atomic number of the material through which the gamma rays pass, and decreases with increasing energy of the photon.
8.92 Gamma radiation can interact with matter in a third manner, called “pair production.” When a gamma-ray photon with energy in excess of 1.02 MeV passes near the nucleus of an atom, the photon may be converted into matter with the formation of a pair of particles, namely, a positive and a negative electron. As with the photoelectric effect, pair production results in the disappearance of the gamma-ray photon concerned. However, the positive electron soon interacts with a negative electron with the formation of two photons of lower energy than the original one. The occurrence of pair production per atom, as with the other interactions, increases with the atomic number of the material, but it also increases with the energy of the photon in excess of 1.02 MeV.
8.93 In reviewing the three types of interaction described above, it is seen that, in all cases, the magnitude per atom increases with increasing atomic number (or atomic weight) of the material through which the gamma rays pass. Each effect, too, is accompanied by either the complete removal of photons or a decrease in their energy. The net result is some attenuation of the gamma-ray intensity or dose rate. Since there is an approximate parallelism between atomic weight and density, the number of atoms per unit volume does not vary greatly from one substance to another. Hence, a given volume (or thickness) of a material containing elements of high atomic weight (”heavy elements”) will be more effective as a gamma-ray shield than the same volume (or thickness) of one consisting only of elements of low atomic weight (”light elements”). An illustration of this difference in behavior will be given below.
8.94 Another important point is that the probabilities of the Compton and photoelectric effects (per atom) both decrease with increasing energy of the gamma-ray photon. However, pair production, which starts at 1.02 MeV, increases with the energy beyond this value. Combination of the various attenuating effects, two of which decrease whereas one increases with increasing photon energy, means that, at some energy in excess of 1.02 MeV, the absorption of gamma radiation by a particular material should be a minimum. That such minima do exist will be seen shortly.
GAMMA-RAY ATTENUATION COEFFICIENTS
8.95 When a narrow (or collimated) beam of gamma rays passes through a material, photons are removed as a result of the Compton scattering interaction as well as by the photoelectric and pair-production interactions. In other words, the scattered photons are regarded as being lost from the beam, although only part of their energy will have been deposited in the material. If such a collimated beam of gamma rays of a specific energy, having an initial intensity (or flux) of $I_0$ photons per square centimeter per second, traverses a thickness of x of a given material, the intensity, $I$, of the rays which emerge without having undergone any interactions can be represented by the equation
where $\mu$ is called the “linear attenuation coefficient.” The distance $x$ is usually expressed in centimeters, so that the corresponding units for $\mu$ are reciprocal centimeters (cm-1). It can be seen from the equation (8.95.1) that, for a given thickness $x$ of material, the intensity $I$ of the emerging gamma rays will be less the larger is the value of $\mu$. In other words, the linear attenuation coefficient is a measure of the shielding ability of a definite thickness, e.g., 1 cm, 1 foot, or other thickness, or any material for a collimated beam of monoenergetic gamma rays.
8.96 The value of $\mu$, under any given conditions, can be obtained with the aid of equation (8.95.1) by determining the gamma-ray intensity before ($I_0$) and after ($I$) passage through a known thickness, $x$, of material. Some of the data obtained in this manner, for monoenergetic gamma rays with energies ranging from 0.5 MeV to 10 MeV, are recorded in Table 8.96. The values given for concrete apply to the common form with a density of 2.3 grams per cubic centimeter (144 pounds per cubic foot). For special heavy concretes, containing iron, iron oxide, or barytes, the coefficients are increased roughly in proportion to the density.
| Linear Attenuation Coefficient (μ) in cm-1 | |||||
|---|---|---|---|---|---|
| Gamma-ray Energy (MeV) | Air | Water | Concrete | Iron | Lead |
| 0.5 | 1.11 × 10-4
| 0.097 |
0.22 |
0.66 |
1.64 |
|
| 1.0 | 0.81 × 10-4
| 0.071 |
0.15 |
0.47 |
0.80 |
|
| 2.0 | 0.57 × 10-4
| 0.049 |
0.11 |
0.33 |
0.52 |
|
| 3.0 | 0.46 × 10-4
| 0.040 |
0.088 |
0.28 |
0.47 |
|
| 4.0 | 0.41 × 10-4
| 0.034 |
0.078 |
0.26 |
0.48 |
|
| 5.0 | 0.35 × 10-4
| 0.030 |
0.071 |
0.25 |
0.52 |
|
| 10 | 0.26 × 10-4
| 0.022 |
0.060 |
0.23 |
0.55 |
|
8.97 By suitable measurements and theoretical calculations, it is possible to determine the separate contributions of the Compton effect ($\mu_c$), of the photo electric effect ($\mu_{pe}$), and of pair production ($\mu_{pp}$) to the total linear attenuation coefficient as functions of the gamma ray energy. The results for lead, a typical heavy element (high atomic number) with a large attenuation coefficient, are given in Fig. 8.97a and those for air, a mixture of light elements (low atomic number) with a small attenuation coefficient, in Fig. 8.97b. Except at extremely low energies, the photoelectric effect in air is negligible, and hence is not shown in the figure. At the lower gamma-ray energies, the linear attenuation coefficients in both lead and air decrease with increasing energy because of the decrease in the Compton and photoelectric effects. At energies in excess of 1.02 MeV, pair production begins to make an increasingly significant contribution. Therefore, at sufficiently high energies the attenuation coefficient begins to increase after passing through a minimum. This is apparent in Fig. 8.97a, as well as in the last column of Table 8.96, for lead. For elements of lower atomic weight, the increase does not set in until very high gamma-ray energies are attained, e.g., about 17 MeV for concrete and 50 MeV for water.
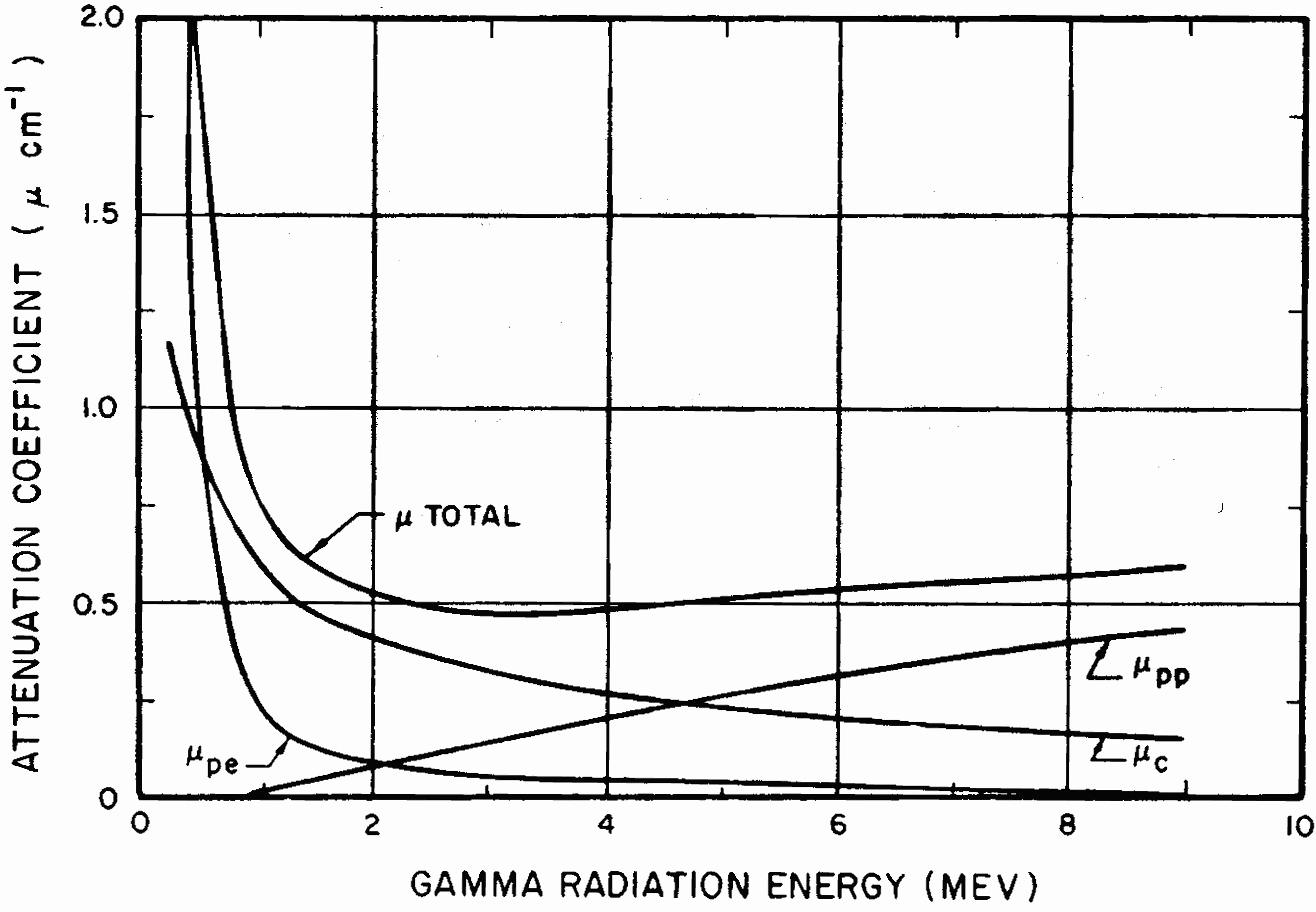
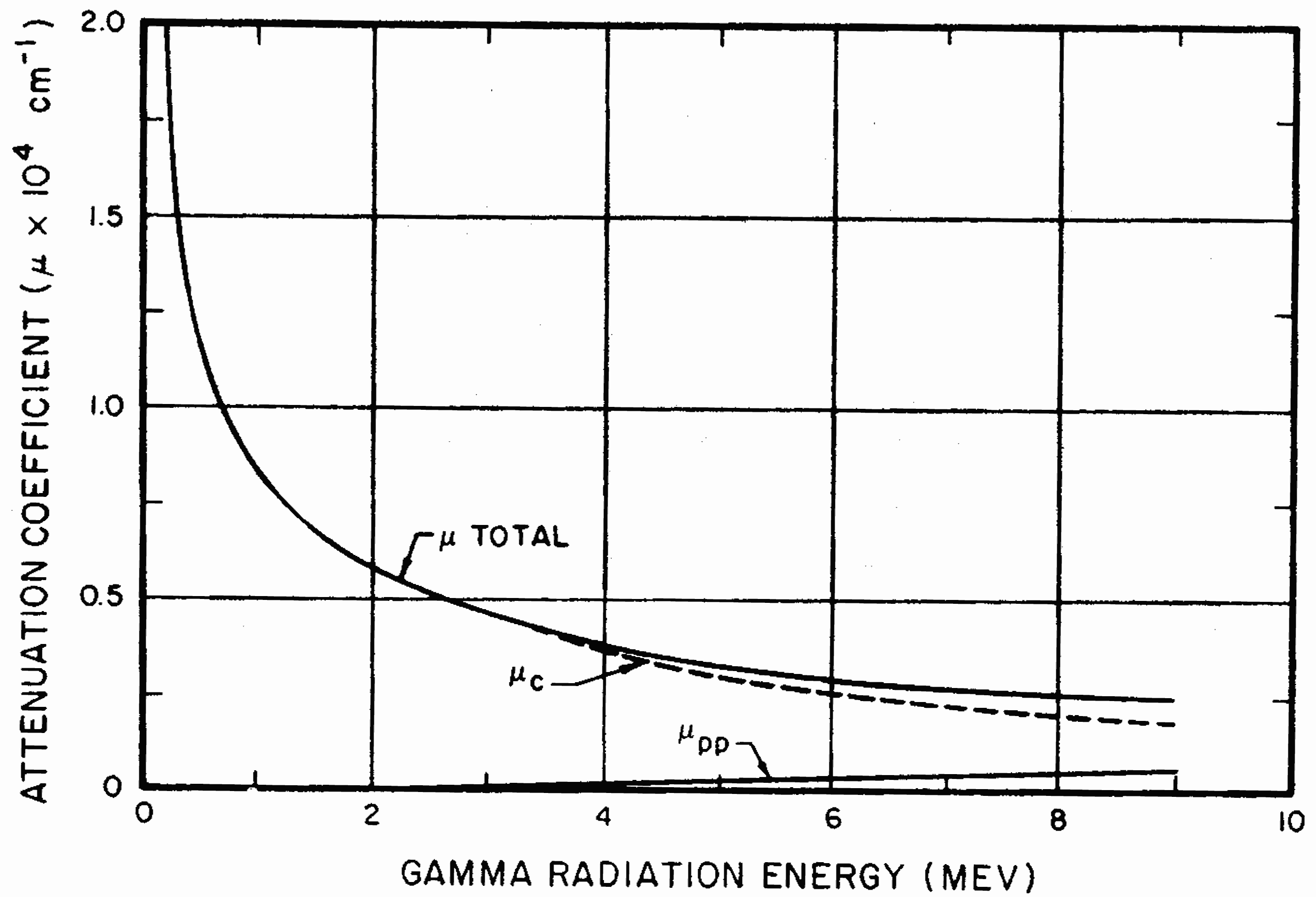
8.98 The fact that the attenuation coefficient decreases as the gamma-ray energy increases, and may pass through a minimum, has an important bearing on the problem of shielding. For example, a shield intended to attenuate gamma rays of 1 MeV energy will be much less effective for radiations of 10 MeV energy because of the lower value of the attenuation coefficient, irrespective of the material of which the shield is composed.
8.99 An examination of Table 8.96 shows that, for any particular energy value, the linear attenuation coefficients increase from left to right, that is, with increasing density of the material. Thus, a given thickness of a denser substance will attenuate the gamma radiation more than the same thickness of a less dense material. This is in agreement with the qualitative concept that a small thickness of a substance of high density will make as effective a gamma-ray shield as a greater thickness of one of lower density (§ 8.38 et seq.).
MASS ATTENUATION COEFFICIENT
8.100 As a very rough approximation, it has been found that the linear attenuation coefficient for gamma rays of a particular energy is proportional to the density of the absorbing (shield) material. That is to say, the linear attenuation coefficient divided by the density, giving what is called the “mass attenuation coefficient,” is approximately the same for all substances for a specified gamma-ray energy. This is especially true for elements of low and medium atomic weight, up to that of iron (about 56), where the Compton effect makes the major contribution to the attenuation coefficient for energies up to a few million electron volts (cf. Fig. 8.97b). For the initial gamma rays of higher energy, the effective mass attenuation coefficient (§ 8.104) is close to 0.023 for water, wood, concrete, and earth, with the densities expressed in grams per cubic centimeter. The value for iron is about 0.027 in the same units (g/cm2).
8.101 If the symbol $\rho$ is used for the density of the shield material, then equation (8.95. l) can be rewritten in the form
where I/I0 is the transmission factor of the shield of thickness $x$ cm, and $\mu/\rho$ is, by definition, the mass attenuation coefficient. Taking $\mu/\rho$ to be 0.023 g/cm2 for initial gamma rays, it follows from equation (8.101.1) that
In the absence of better information, this expression may be used to provide a rough idea of the dose transmission factor, as defined in § 8.72, of a thickness of x centimeters of any material (of known density) of low or moderate atomic weight.
8.102 The simple tenth-value thickness concept described in§ 8.39 is based on equation (8.95.1). For such a thickness the transmission factor is 0.1 and if the thickness is represented by $x_{0.1}$, it follows that
\[ 0.1 = e^{-\mu x_{0.1}} \]or
If $\mu/\rho$ is taken to be 0.023 g/cm2 for the initial gamma radiation of higher energy then, as a “rule-of-thumb” approximation,
\[ x_{0.1} \text{ (cm) } \approx \frac{100}{\rho(\text{g/cm}^3)} \]or the equivalent
where, as in § 8.42, $T$ is the tenth-value thickness in feet and $D$ is the density of the material in lb/ft3. It follows, therefore, that for the less-dense materials, for which $\mu/\rho$ is close to 0.023 g/cm2, the product $D \times T$ should be equal to about 200 lb/ft2 for gamma rays of higher energy. This is in agreement with the values in the last column of Table 8.41 for nitrogen capture (secondary) gamma rays. The $D \times T$ for iron (or steel) is smaller than for the other materials because $\mu/\rho$ is larger, namely about 0.027 g/cm2, for the gamma rays of higher energy.
THICK SHIELDS: BUILDUP FACTOR
8.103 Equation (8.95.1) is strictly applicable only to cases in which the photons scattered in Compton interactions may be regarded as having been removed from the gamma-ray beam. This situation holds reasonably well for narrow beams or for shields of moderate thickness, but it fails for broad beams or thick shields. In the latter circumstances, the photon may be scattered several times before emerging from the shield. For broad radiation beams and thick shields, such as are of interest in shielding from nuclear explosions, the value of $I$, the intensity (or dose) of the emerging radiation, is larger than that given by equation (8.95.1). Allowance for the multiple scattering of the radiation is made by including a “buildup factor,” represented by $B(x)$, the value of which depends upon the thickness $x$ of the shield, the nature of the material, and the energy of the impinging radiation; thus, equation (8.95.1) is now written as
\[ I = I_0 B(x)e^{-\mu x}. \]Values of the buildup factor for a variety of conditions have been calculated for a number of elements from a theoretical consideration of the scattering of photons by electrons. The fact that these values are frequently in the range from 10 to 100 shows that serious errors could arise if equation (8.95.1) is used to determine the attenuation of gamma rays by thick shields.
8.104 It will be apparent, therefore, that equation ( 8.95. l) and others derived from it, such as equations (8.101.2) and (8.102.1), as well as the simple tenth-value thickness concept, will apply only to monoenergetic radiation and thin shields, for which the buildup factor is unity. By taking the mass attenuation coefficient to be O.023 for less dense materials (or 0.027 for iron), as given above, an approximate (empirical) allowance has been made for both the polyenergetic nature of the gamma radiations from a nuclear explosion and the buildup factors due to multiple scattering of the photons. The results are, at best, applicable only to shields with simple (slab) geometries. Furthermore, practical radiation shields must absorb neutrons as well as gamma rays, and the gamma radiation produced in the shield by inelastic scattering and radiative capture of the neutrons may produce a greater intensity inside the shield than the incident gamma radiation. Consequently, any problem involving gamma radiation shielding, especially in the presence of neutrons, is complex, even for relatively simple structures; appropriate computer codes are thus necessary to obtain approximations of the attenuation. In the absence of better information, however, the effective tenth-value thicknesses, as given in Table 8.41 or derived from equation (8.102.2), can be used to provide a rough indication of gamma-ray shielding.
THE INITIAL GAMMA-RAY SPECTRUM
8.105 The major proportion of the initial gamma radiation received at a distance from a nuclear explosion arises from the interaction of neutrons with nuclei, especially nitrogen, in the atmosphere and from the fission products during the first minute after the burst. Gamma rays from inelastic scattering and neutron capture by nitrogen have effective energies ranging up to 7.5 MeV (or more) and those from the fission products are mainly in the 1 to 2 MeV range. After passage through a distance in air, some of the photons will have been removed by photoelectric and pair-production effects and others will have had their energies decreased as a result of successive Compton scattering. There will consequently be a change in the gamma-ray energy distribution, i.e., in the spectrum.
8.106 Information concerning the gamma-ray spectrum of the initial radiation is important because the susceptibility of living organisms and of various electronics components, the attenuation properties of air and shielding materials, and the response of radiation detectors are dependent upon it. Although the interactions of both neutrons and gamma rays with the atmosphere, which determine the gamma-ray spectrum, are complex, it is possible to calculate the spectrum at various distances from a nuclear explosion. Computations of this kind have been used to estimate gamma-ray doses, as will be seen later (§ 8.125 et seq.). As an example, Fig. 8.106 shows the spectrum of the initial gamma radiation received at a distance of 2,000 yards from the explosion of a fission weapon with an energy yield of 20 kilotons. At this range, some 70 percent of the gamma-ray photons have energies less than 0.75 MeV. It should be remembered, however, that the photons of high energy are the most hazardous and also are the most difficult to attenuate.
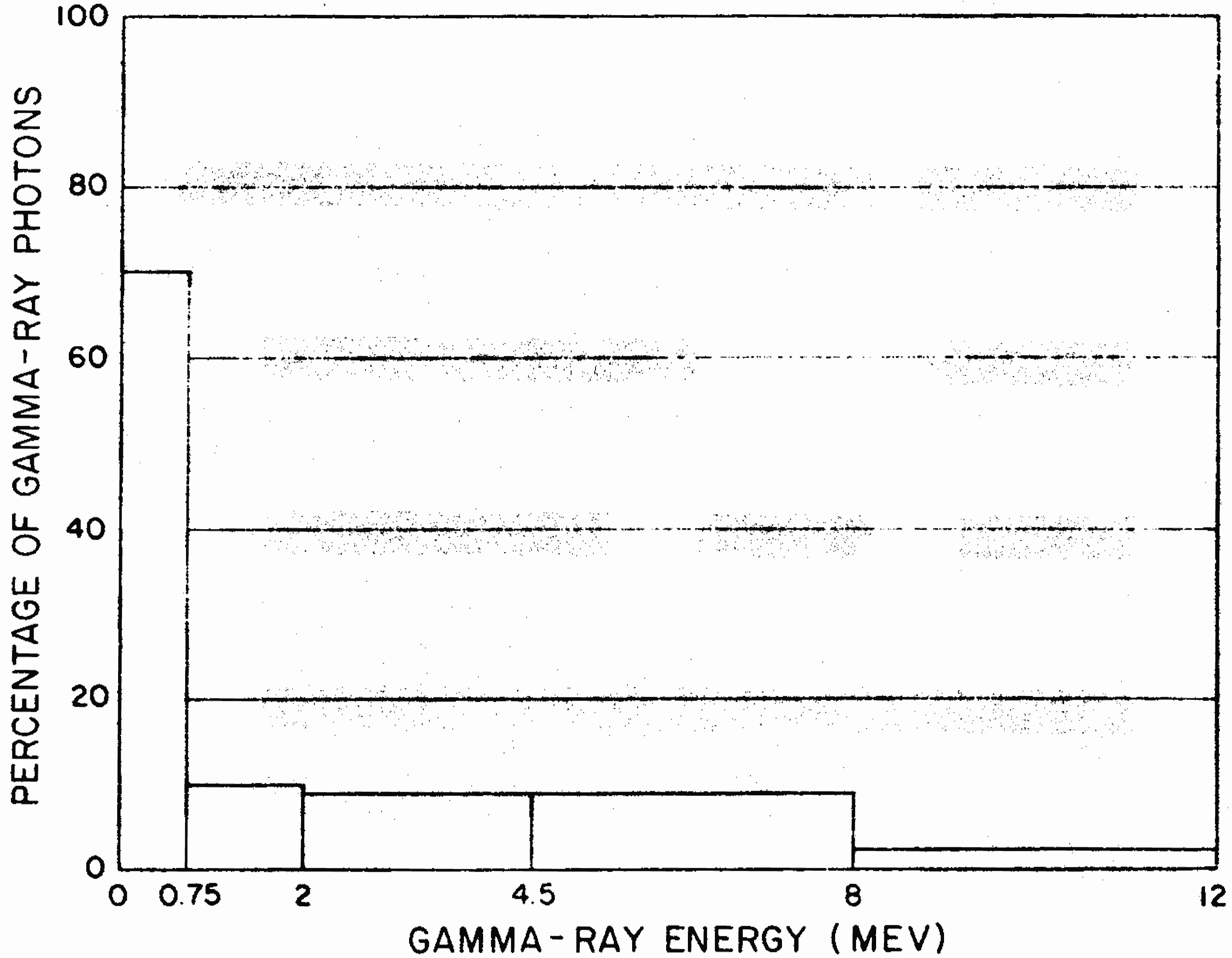
INTERACTIONS OP NEUTRONS WITH MATTER
8.107 The modes of interaction of neutrons with matter are quite different from those experienced by gamma-ray photons. Unlike photons, neutrons are little affected by electrons, but they do interact in various ways with the nuclei of atoms present in all forms of matter. These neutron-nucleus interactions are of two main types, namely, scattering and absorption. As already seen, scattering reactions can be either inelastic (§ 8.09) or elastic (§ 8.52). In inelastic scattering part of the kinetic energy of the neutron is converted into internal (or excitation) energy of the struck nucleus; this energy is then emitted as gamma radiation. For inelastic scattering to occur, the neutron must initially have sufficient energy to raise the nucleus to an excited state. The magnitude of this energy depends on the nature of the nucleus and varies greatly from one element to another. However, a rough general rule is that for many, but not all, heavy or moderately heavy nuclei, e.g., iron and uranium, inelastic scattering may occur for neutrons with energies ranging from a few tenths MeV to as low as a few tens of keV. For lighter nuclei, inelastic scattering is possible only when the neutrons have higher energies. Significant inelastic scattering occurs only for neutron energies above about 1.6 MeV for nitrogen and about 6 MeV for oxygen. Neutrons with energies below the appropriate threshold values for the nuclei present in the medium cannot undergo inelastic scattering.
8.108 When elastic scattering occurs, the interaction of the neutron with a nucleus is equivalent to a collision between two billiard balls; kinetic energy is conserved and is merely transferred from one particle to the other. None of the neutron energy is transformed into excitation energy of the nucleus and there is no accompanying gamma radiation. In contrast with inelastic scattering, elastic scattering can take place with neutrons of all energies and any nucleus. For a given angle of impact, the fraction of the kinetic energy of the neutron that is transferred to the nucleus in a collision is dependent only on the mass of the latter. The smaller the mass of the nucleus the greater is the fraction of the neutron energy it can remove. Theoretically, the whole of the kinetic energy of a neutron could be transferred to a hydrogen nucleus (proton) in a single head-on collision. In fact, hydrogen, the lightest element, offers the best means for rapidly degrading fast neutrons with energies less than about 0.5 MeV. It is for this reason that hydrogen, e.g., as water, is an important constituent of neutron shields(§ 8.67). For neutrons of higher energy than 0.5 MeV, it is better to take advantage of inelastic scattering to slow down the neutrons. The heavy element in the special concretes described in § 8.69 serves this purpose.
8.109 The second fundamental type of interaction of neutrons with matter involves complete removal of the neutron by capture. Radiative capture (§ 8.08) is the most common kind of capture reaction; it occurs to some extent, at least, with nearly all nuclei. The probability of capture is greater for slow neutrons than for those of high energy. Most light nuclei, e.g., carbon and oxygen, have little tendency to undergo the radiative capture reaction with neutrons. With nitrogen, however, the tendency is significant (§ 8.11), but not great. For other nuclei, especially some of medium or high mass, e.g., cadmium, the radiative capture reaction occurs very readily. In certain cases, the reaction product is radioactive (§ 8.61); this is of importance in some aspects of weapons effects, as will be seen in Chapter IX.
8.110 Another type of reaction is that in which the incident neutron enters the target nucleus and the compound nucleus so formed has enough excitation energy to permit the expulsion of another (charged) particle, e.g., a proton, deuteron, or alpha particle. The residual nucleus is often in an excited state and emits the excess energy as a gamma-ray photon. This type of reaction usually occurs with light nuclei and fast neutrons, although there are a few instances, e.g., lithium-6 and boron-IO, where it also takes place with slow neutrons. Nitrogen interacts with fast neutrons in at least two ways in which charged particles are emitted (§§ 9.34, 9.44); one leads to the formation of radioactive carbon-14 (plus a proton) and the other to tritium, the radioactive isotope of hydrogen (plus stable carbon-12).
8.111 Fission is, of course, also a form of interaction between neutrons and matter. But since it is restricted to a small number of nuclear species and has been considered in detail in Chapter I, it will not be discussed further here.
8.112 The rate of interaction of neutrons with nuclei can .be described quantitatively in terms of the concept of nuclear “cross sections.” The cross section may be regarded as the effective target area of a particular type of nucleus for a specific reaction and is a measure of the probability that this reaction will occur between a neutron, of given energy, and that nucleus. Thus, each nuclear species has a specific scattering cross section, a capture cross section, and so on, for a given neutron energy; the total cross section for that energy is the sum of the specific cross sections for the individual interactions. Both specific and total cross sections vary with the energy of the neutron, often in a very complex manner.
8.113 The nuclear cross sections for neutron-nucleus interactions are analogous to the linear attenuation coefficients (for gamma rays) divided by the number of nuclei in unit volume of the medium. In fact, an expression similar to equation (8.95.1) can be employed to describe the attenuation of a narrow beam of monoenergetic neutrons in their passage through matter. However, because the neutrons in the initial nuclear radiation are far from monoenergetic and the cross sections are so highly dependent on the neutron energy, the equivalent of equation (8.95.1) must not be used to calculate neutron attenuation for shielding purposes. Shielding calculations can be made by utilizing cross sections, the neutron energy distribution in space and direction, and other data, but the calculations require the use of computer codes. Such calculations are too complicated to be described here.
THE NEUTRON ENERGY SPECTRUM
8.114 The energies of the neutrons received at some distance from a nuclear explosion cover a very wide range, from several millions down to a fraction of an electron volt. The determination of the complete energy spectrum (§ 8.53), either by experiment or by calculation, is very difficult. However, it is possible to divide the spectrum into a finite number of energy groups and to calculate the neutron flux in each energy group at various distances from the explosion point. These calculations can then be checked by measuring the variation of flux with distance from known neutron sources that are representative of each energy group.
8.115 Prior to the cessation of atmospheric testing of nuclear weapons, neither the extremely large and fast computers nor the sophisticated measurement instruments that are now available were in existence. Recourse was, therefore, made to measurements of neutron flux within a few specified energy ranges; from the results a general idea of the spectrum was obtained. Measurements of this kind were made by the use of threshold detectors of activated foil or fission foil type (§§ 8.61, 8.62).
8.116 Neutrons are liberated during the fission and fusion processes, but the neutrons of interest here are those that escape from the exploding weapon. Both the total number of neutrons and their spectrum are altered during transit through the weapon materials. Output spectra that might be considered illustrative of fission and thermonuclear weapons are shown in Figs. 8.116a and b, respectively. As mentioned previously, the neutron source can be defined properly only by considering the actual design of a specific weapon. Hence, the spectra in these figures are presented only as examples and should not be taken to be generally applicable.
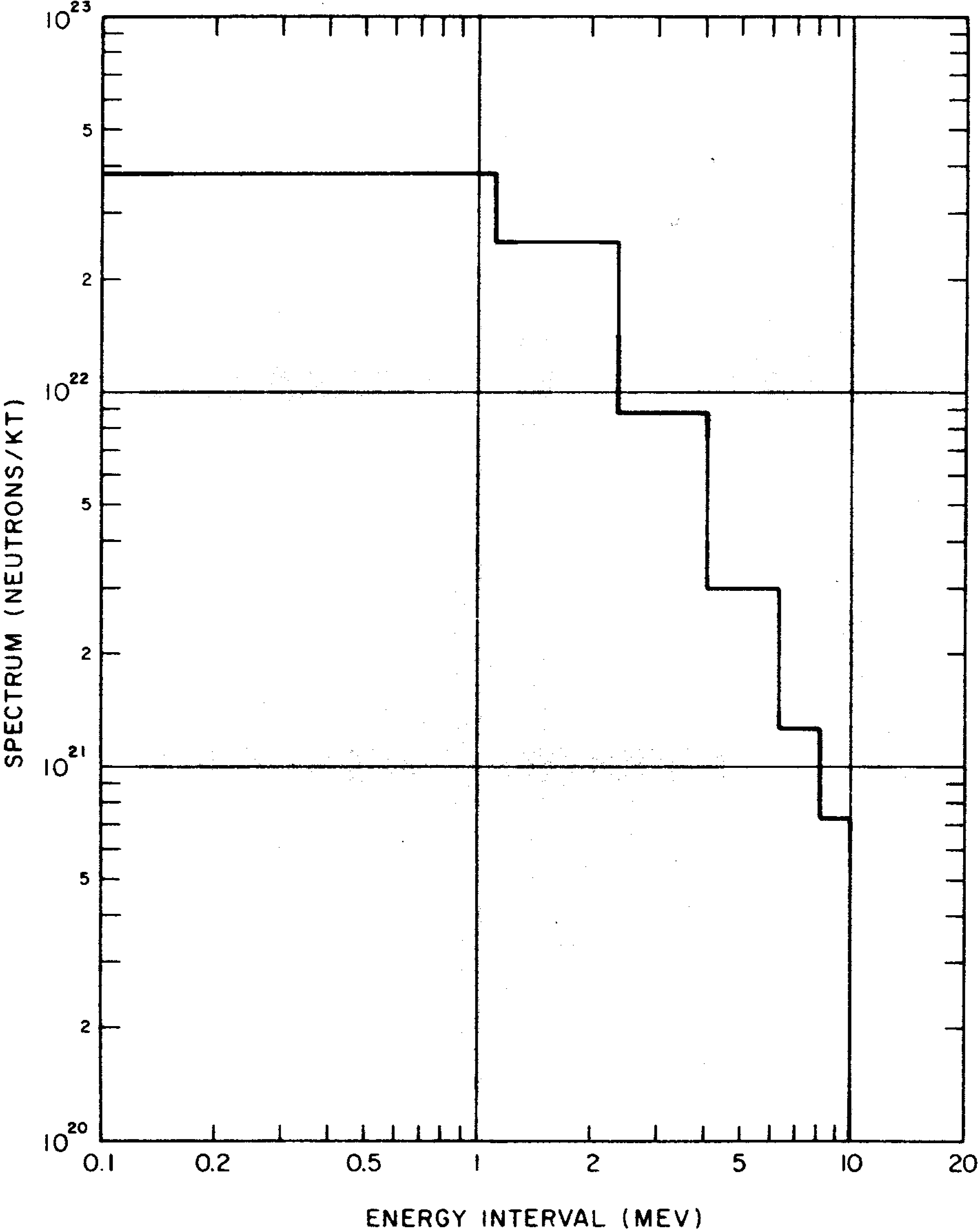

8.117 Passage of the neutrons through the air, from the exploding weapon to a distant point, is accompanied by interactions with nuclei that result in attenuation and energy changes. Hence, the neutron spectrum at a distance may differ from the output spectrum of the weapon. Extensive results of computer calculations of neutron fluences at (or near) the earth’s surface are now available and these have been used to plot the curves in Figs. 8.117a and b, for fission and thermonuclear weapons, respectively. The figures show the neutron fluences per kiloton of energy release for a number of energy groups as a function of slant range. The uppermost curve in each case gives the total fluence (per kiloton) of neutrons with energies greater than O.0033 MeV, i.e., 3.3 keV.
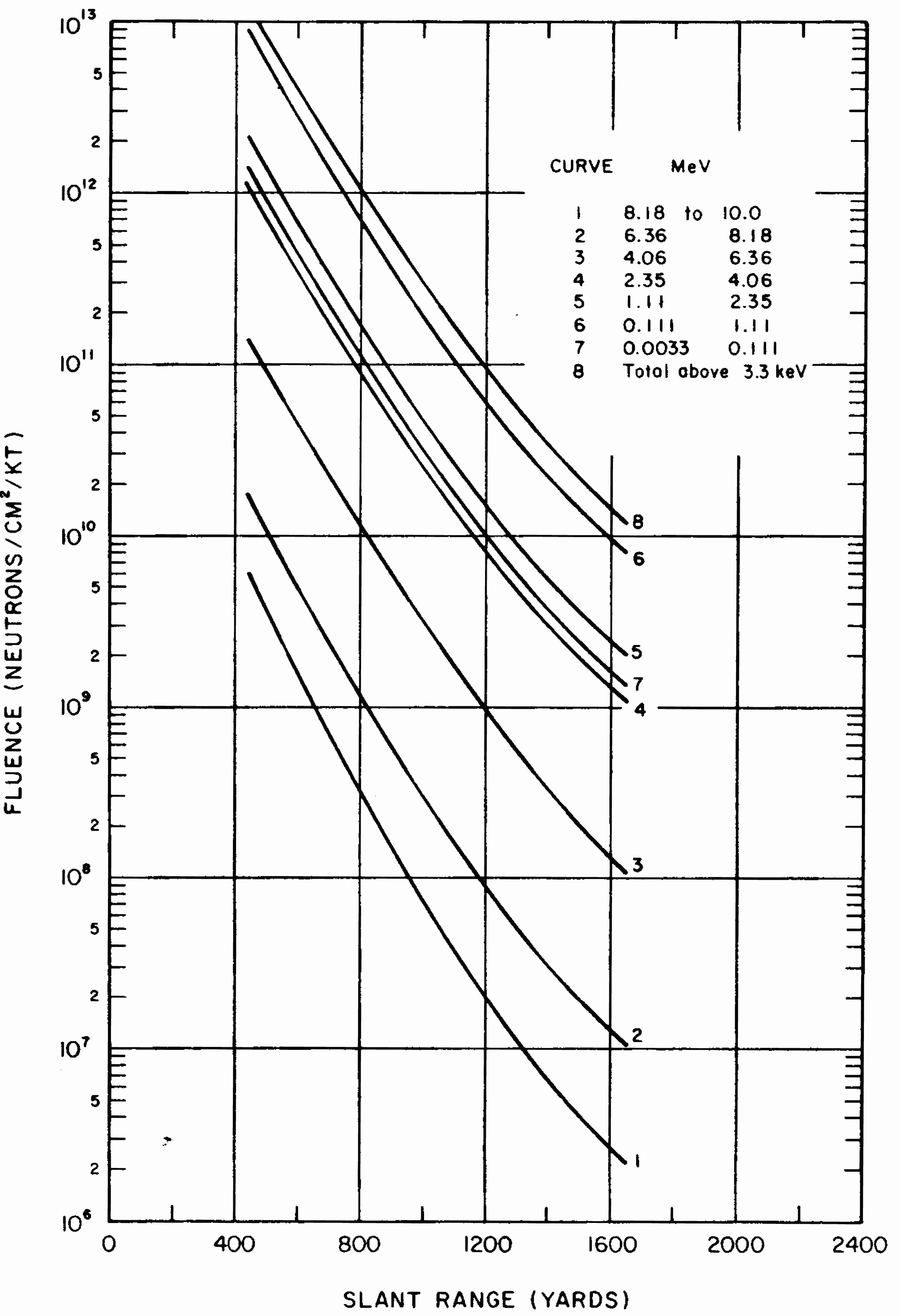
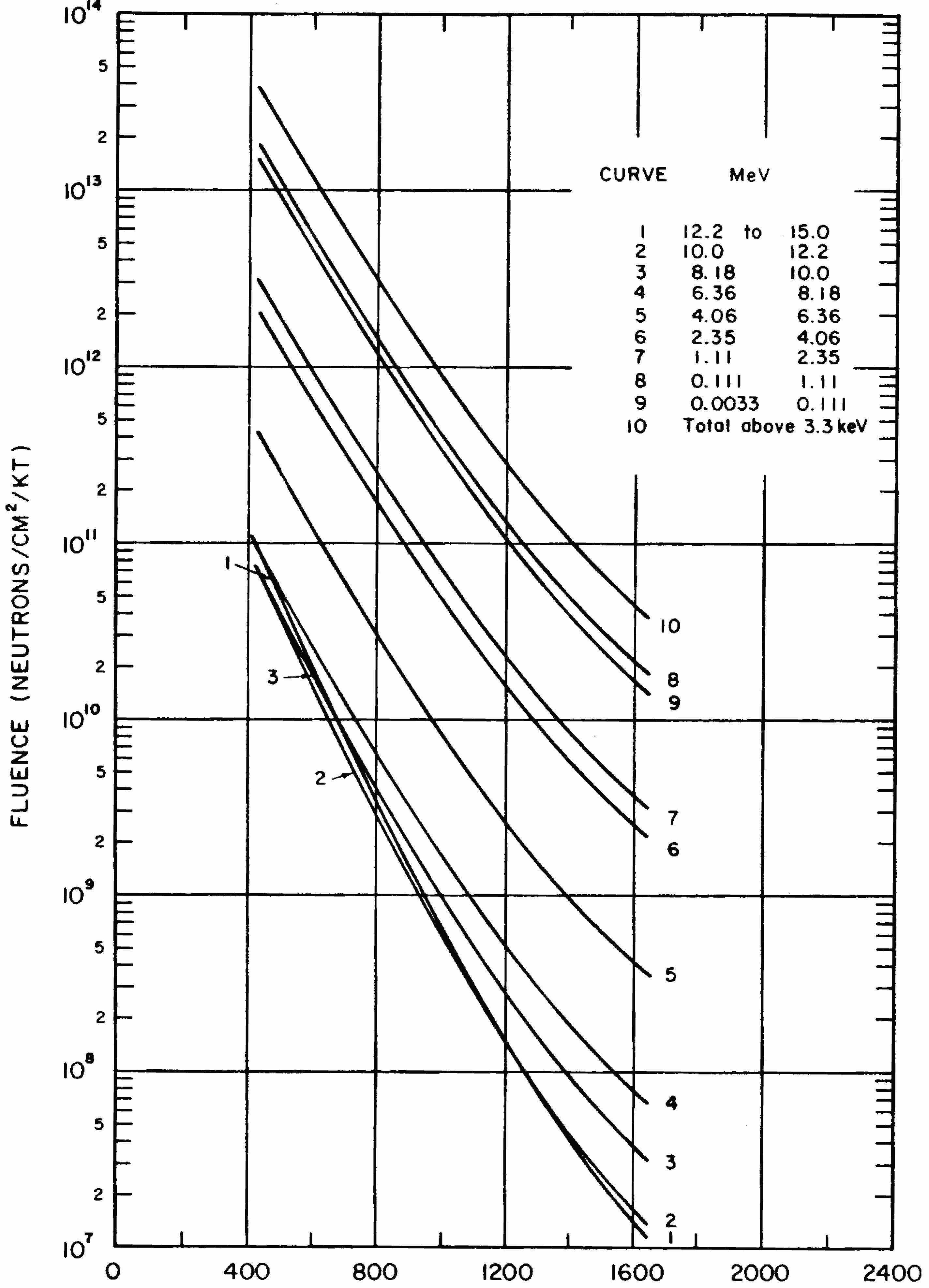
8.118 It is apparent from Fig. 8.117a that for a fission weapon the curves for the different energy groups all have roughly the same slope. This means that the fluence in each energy group decreases with increasing distance from the explosion, but the proportions in the various groups do not change very much; that is to say, the neutron spectrum does not vary significantly with distance. Furthermore, although it is not immediately apparent from Fig. 8.117a, the spectrum is almost the same as the source spectrum in Fig. 8.116a. This accounts for the equilibrium neutron spectrum from a fission explosion mentioned in § 8.55. The spectrum does change at much lower neutron energies, but this is not important.
8.119 Examination of Fig. 8.117b for thermonuclear weapons reveals a different behavior. Curves 5 through 9, i.e., for neutron energies from 0.0033 to 6.36 MeV, are almost parallel, so that in this range the spectrum does not change much with distance. But at higher energies, especially from 8.18 to 15 MeV, the slopes of the curves are quite different. Of the neutrons in groups 1, 2, and 3, those in group 1 , which have the highest energies, predominate at a slant range of 400 yards, but they are present in the smallest proportion at 1,600 yards. During their passage through the air, the fastest neutrons are degraded in energy and their relative abundance is decreased whereas the proportions of the somewhat less energetic neutrons is increased. The neutron spectrum thus changes with distance, especially in the high-energy range. The peak that exists at 12 to 14 MeV of the source spectrum in Fig. 8.116b becomes lower and the valley between about 6 and 12 MeV disappears with increasing slant range. At very long ranges, when the high-energy neutrons have lost much of their energy, an equilibrium spectrum would be approached.
8.120 Figs. 8.117a and b provide estimates of neutron fluences and spectra from low air bursts for targets on or near the surface of the ground. As a result of reflections and absorption by the ground, an air-ground interface can increase or decrease the neutron fluences by as much as a factor of ten compared to fluences at corresponding distances in an infinite air medium. For source-target separation distances less than about a relaxation length,14 localized reflection from the ground generally tends to increase the intensity of high-energy neutrons; however, at such short distances, the initial nuclear radiation is of interest only for very low yields, since for higher yields other weapon effects will normally be dominant (cf. § 8.06). At longer distances, the high-energy neutron intensity may be reduced by a factor of five or more compared to infinite air when both the source and the target are at or near the ground surface, e.g. a surface or near surface burst. These effects have been included in the calculations from which the figures given above were derived.
INITIAL RADIATION DOSE IN TISSUE
8.121 Simplified, but reasonably accurate, methods have been developed to predict the initial radiation dose to persons located on or near the surface of the earth. These methods are described separately for neutrons, secondary gamma rays from radiative capture and inelastic scattering in the atmosphere(§ 8.11), and fission product gamma rays. The contribution of the primary gamma rays from fission to the radiation dose at a distance is small enough to neglect (§ 8.04). In all cases, the data are based on the assumption that the average density of the air in the transmission path, between the burst point and the target, is 0.9 of the normal sea-level density.
Initial Neutron Absorbed Dose
8.122 With spectra such as those shown in Figs. 8.116a and b to serve as sources, a neutron transport computer code may be used to calculate the neutron dose resulting from a nuclear explosion in a specified geometry, i.e., burst height, target height, and air density. The latter is taken to be the average density of the air between the burst and the target before disturbance of the air by the blast wave, since the neutrons of interest depart from the region of the explosion before formation of the blast wave and are deposited at the target prior to its arrival.
8.123 Results of such calculations, which have been corroborated by test data, are given in Figs. 8.123a and b, for fission and thermonuclear weapons, respectively. In each case the absorbed neutron dose (in tissue) received by a target on or near the surface of the earth is shown as a function of slant range per kiloton energy yield for explosions at a height of about 300 feet or more. For convenience of representation, the curves are shown in two parts; the left ordinate scale is for shorter ranges and the right is for longer distances. For fission weapons, there are two curves in each part; they do not necessarily represent the extremes in neutron dose that might result from different weapon designs, but the dose from most fission weapons should fall between the two curves. It is suggested that the upper curve of each pair in Fig. 8.123a be used to obtain a conservative estimate of the neutron dose from fission weapons for defensive purposes and that the lower curve be used for a conservative estimate for offensive purposes.
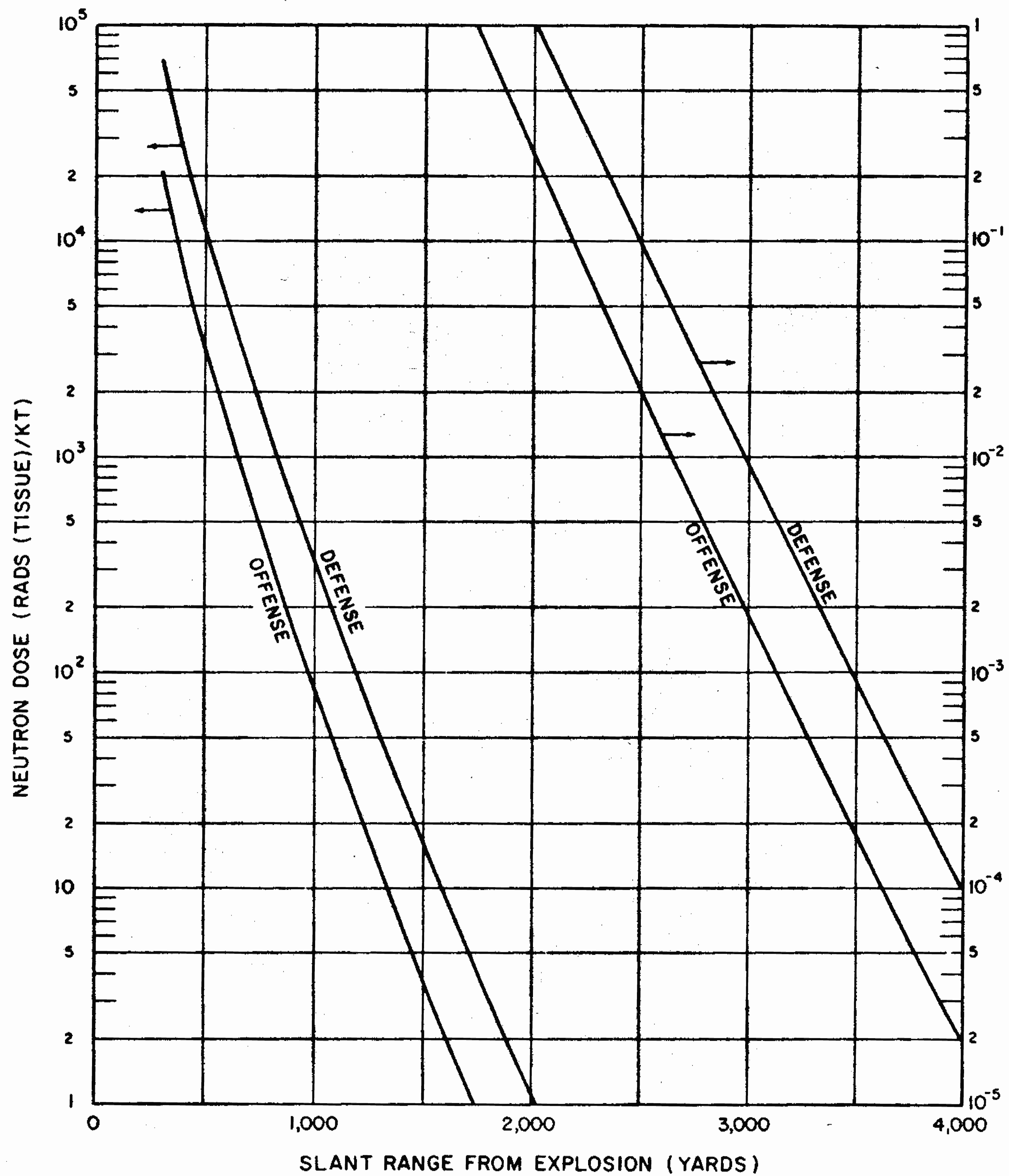
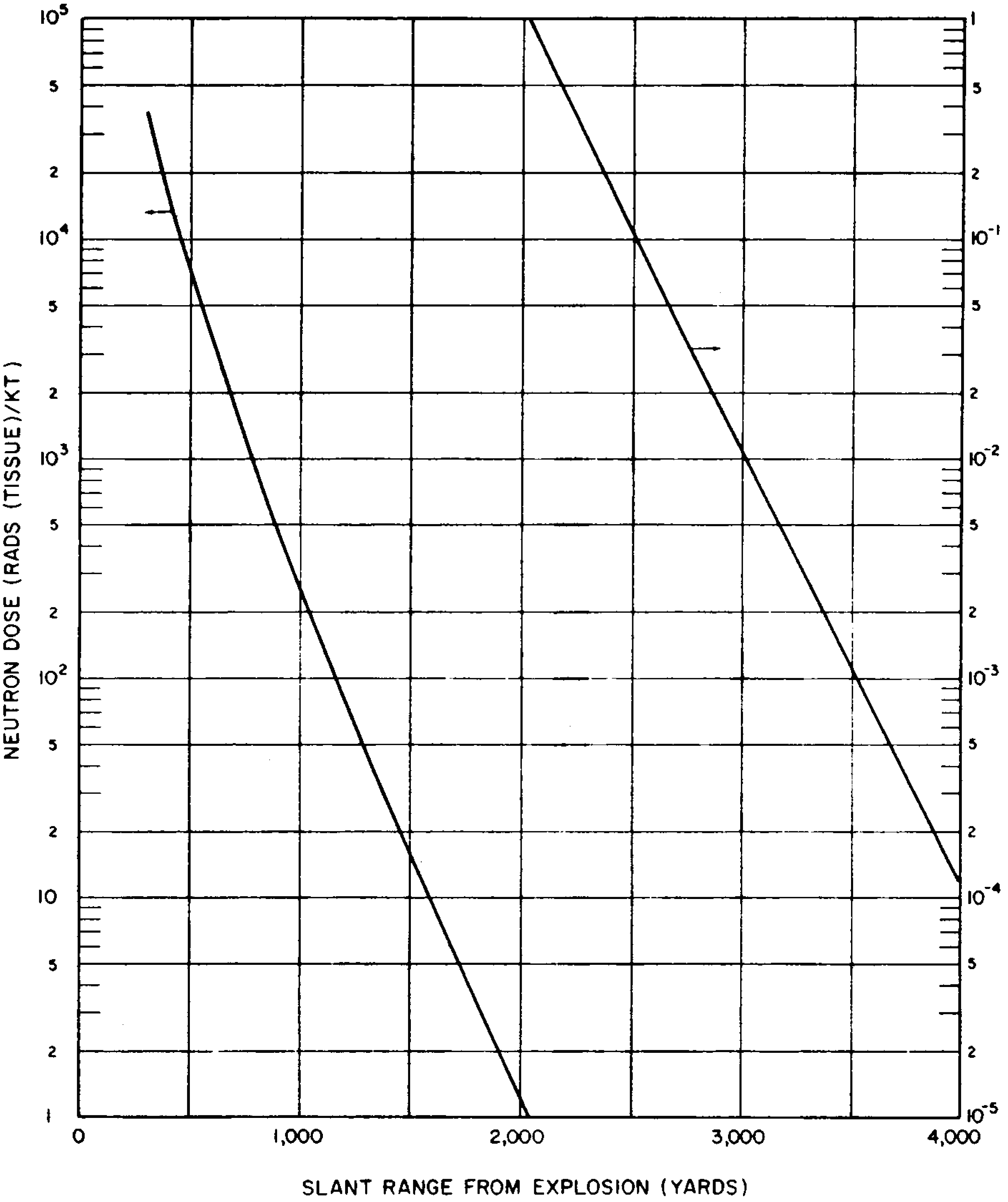
8.124 In order to determine the neutron dose received from an air burst of $W$ kilotons energy yield, the dose for the given distance as obtained from Fig. 8.123a or b is multiplied by W. For a contact surface burst, the values from Figs. 8.123a and b should be multiplied by 0.5. For explosions above the surface but below about 300 feet, an approximate value of the neutron dose may be obtained by linear interpolation between the values for a contact surface burst and one at 300 feet or above. The “defense” curve of Fig. 8.123a was used to generate the data for Fig. 8.64a, and the curve in Fig. 8.123b was used for Fig. 8.64b.
Secondary Gamma-Ray Absorbed Dose
8.125 The secondary (or air-secondary) gamma rays, i.e., the gamma rays produced by various interactions of neutrons with atmospheric nuclei, must be considered separately from the fission product gamma rays to provide a generalized prediction scheme since the relative importance of the two depends on several factors, including the total yield, the fraction of the total yield derived from fission, the height of burst, and the slant range from the explosion to the target. Since measurements at atmospheric tests have provided only the total gamma radiation dose as a function of distance from the source, computer calculations have been used to obtain the doses from the two individual gamma-ray sources. The results of the calculations of air-secondary gamma ray doses (and the total doses) predicted by the calculations have been compared with measurements performed at nuclear weapon tests. For bursts in the lower atmosphere, the gamma rays from isomeric decay provide such a small fraction of the total gamma-ray energy that they can be neglected in the calculation of total dose in tissue.15
8.126 By using neutron spectra, such as those shown in Figs. 8.116a and b, the secondary gamma-ray source can be calculated. The latter is then utilized to compute the secondary gamma-ray dose resulting from a nuclear explosion in a specified geometry. As is the case for neutrons, the air density is taken to be the average density of the air between the burst and the target before disturbance of the air by the blast wave, since the secondary gamma rays reach a distant target before the blast wave has traveled very far (see Fig. 8.14).
8.127 Some of the results of calculations of secondary absorbed gamma ray doses (in tissue), obtained in the manner indicated above, are shown in Figs. 8.127a and b, which correspond to the neutron dose curves in Figs. 8.123a and b, respectively. The conditions of applicability of the figures, such as air burst or contact surface burst, target location, offensive or defensive use, etc., are the same as given in §§ 8.123, 8.124. In order to be consistent, if either the “offense” or “defense” curve in Fig. 8.123a is used to obtain the neutron dose for a given situation, the corresponding curve in Fig. 8.127a should be used for the secondary gamma-ray dose.
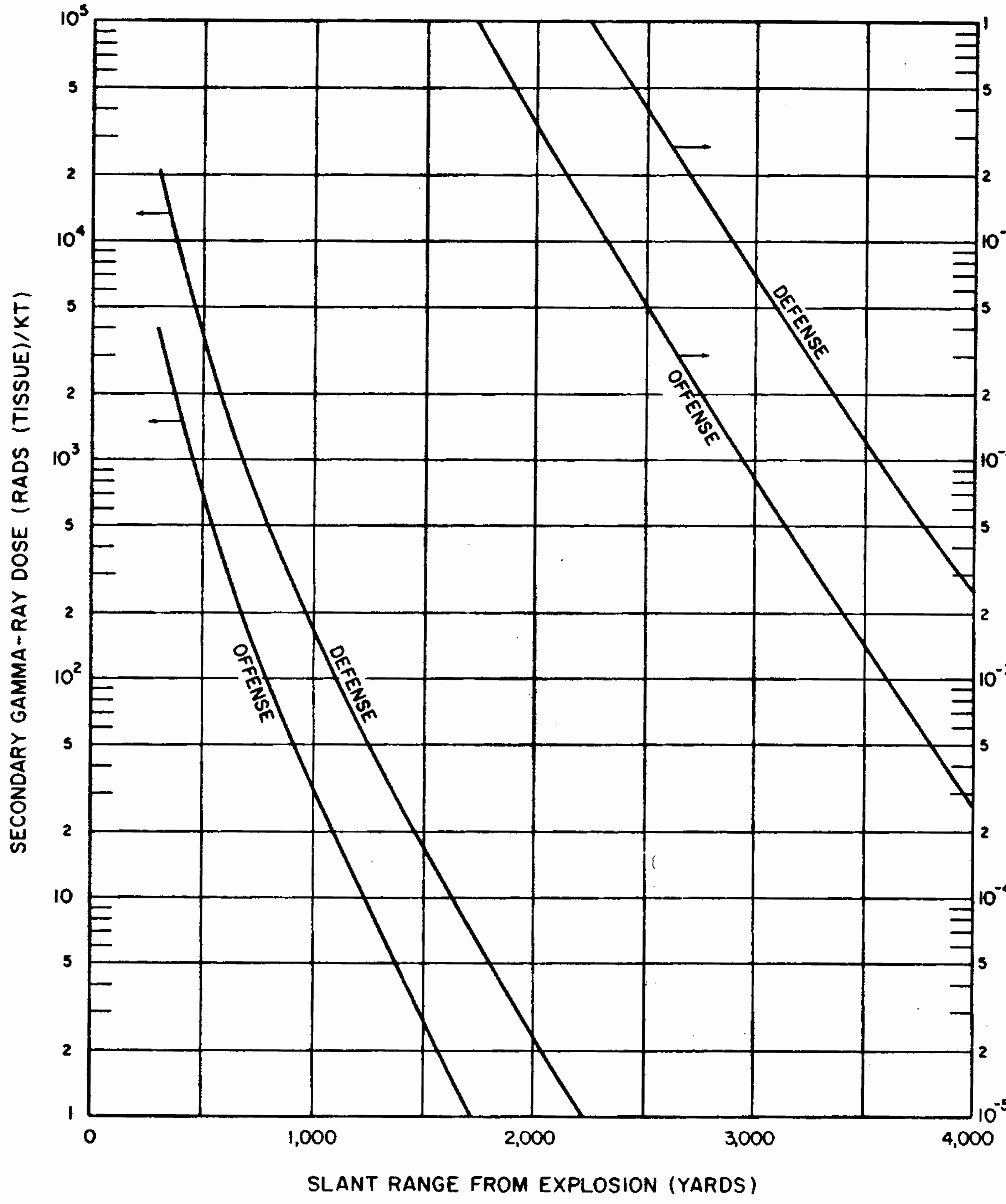
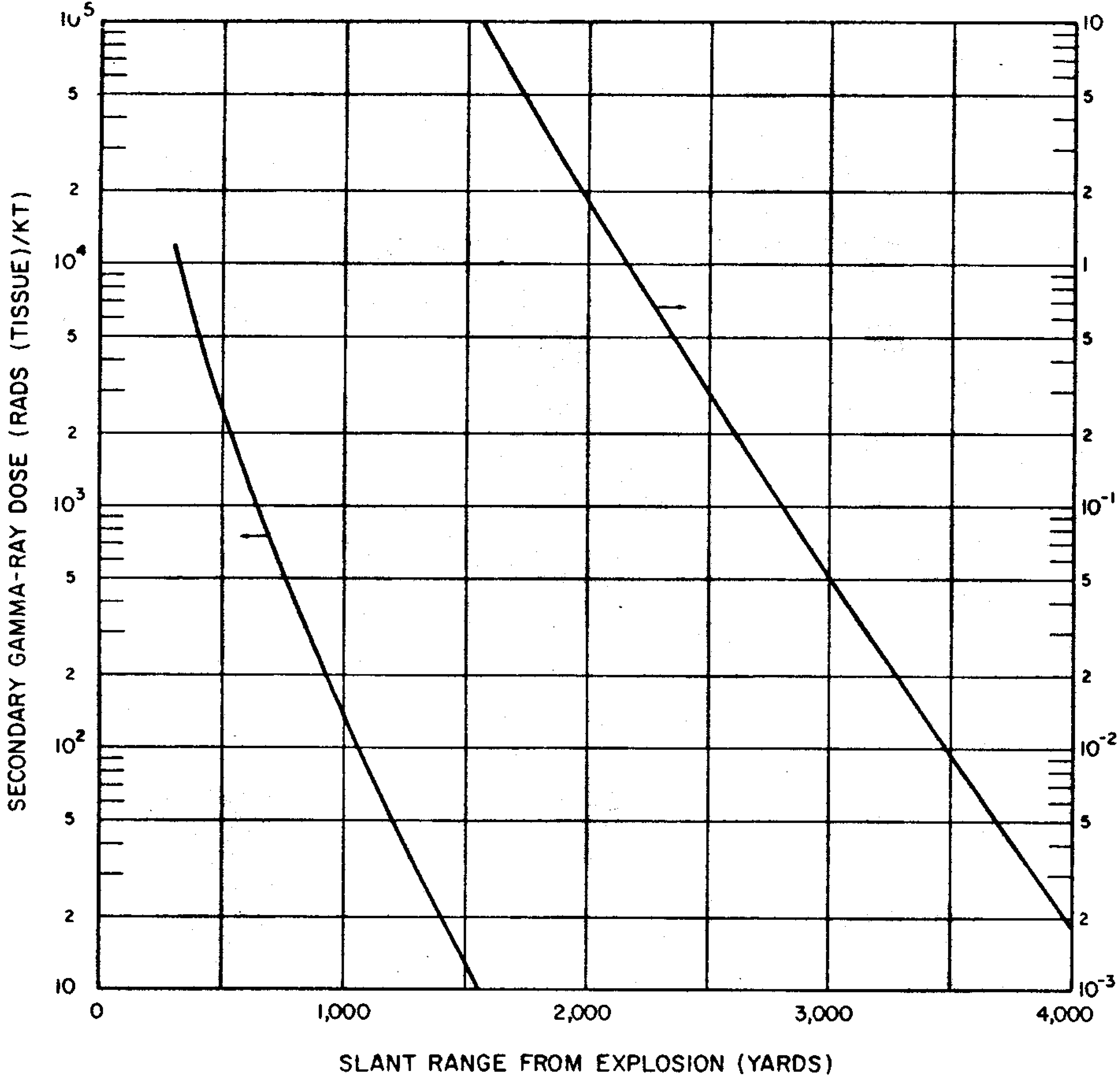
Fission Product Gamma-Ray Absorbed Dose
8.128 In order to estimate the gamma-ray dose from fission products, the radiation transport computer code must be supplemented with a code that describes the evolution and rise of the radioactive cloud containing the fission products. Since the fission product radiation is emitted over a sufficiently long period of time, the hydrodynamic effect (§ 8.36) of the blast wave on the average air density between the source and the target must be considered. The hydrodynamic enhancement becomes more important at high energy yields and also at greater ranges because of the larger volume of low-density air behind the shock front.
8.129 With minimal hydrodynamic enhancement, as is the case for very low-yield weapons, the fission product gamma rays and the secondary gamma rays contribute approximately equal doses at slant ranges up to about 3,000 yards. However, the average energy of the former gamma rays is considerably less than that of the latter, and the angular distribution of the fission product gamma rays is diffused by the rise of the cloud. Each of these factors tends to reduce the dose from fission product gamma rays relative to that from secondary gamma rays with increasing distance from low-yield explosions. For explosions of higher yield, however, hydrodynamic enhancement may cause the fission product gamma-ray dose to exceed the secondary gamma-ray dose, particularly at longer ranges.
8.130 The calculated fission product gamma-ray dose in tissue per kiloton of fission energy yield received by a target on or near the surface of the earth as a function of slant range from a nuclear explosion is shown in Fig. 8.130a. In order to determine the fission product gamma-ray dose received in the initial radiation from an air burst of a fission weapon of W kilotons energy yield, the value for the given distance as obtained from Fig. 8.130a is multiplied by the “effective” yield, determined from Fig. 8.130b. The use of the effective yield instead of the actual yield provides the necessary corrections for the differences in cloud rise velocity and the hydrodynamic enhancement, each of which is a function of total energy yield.
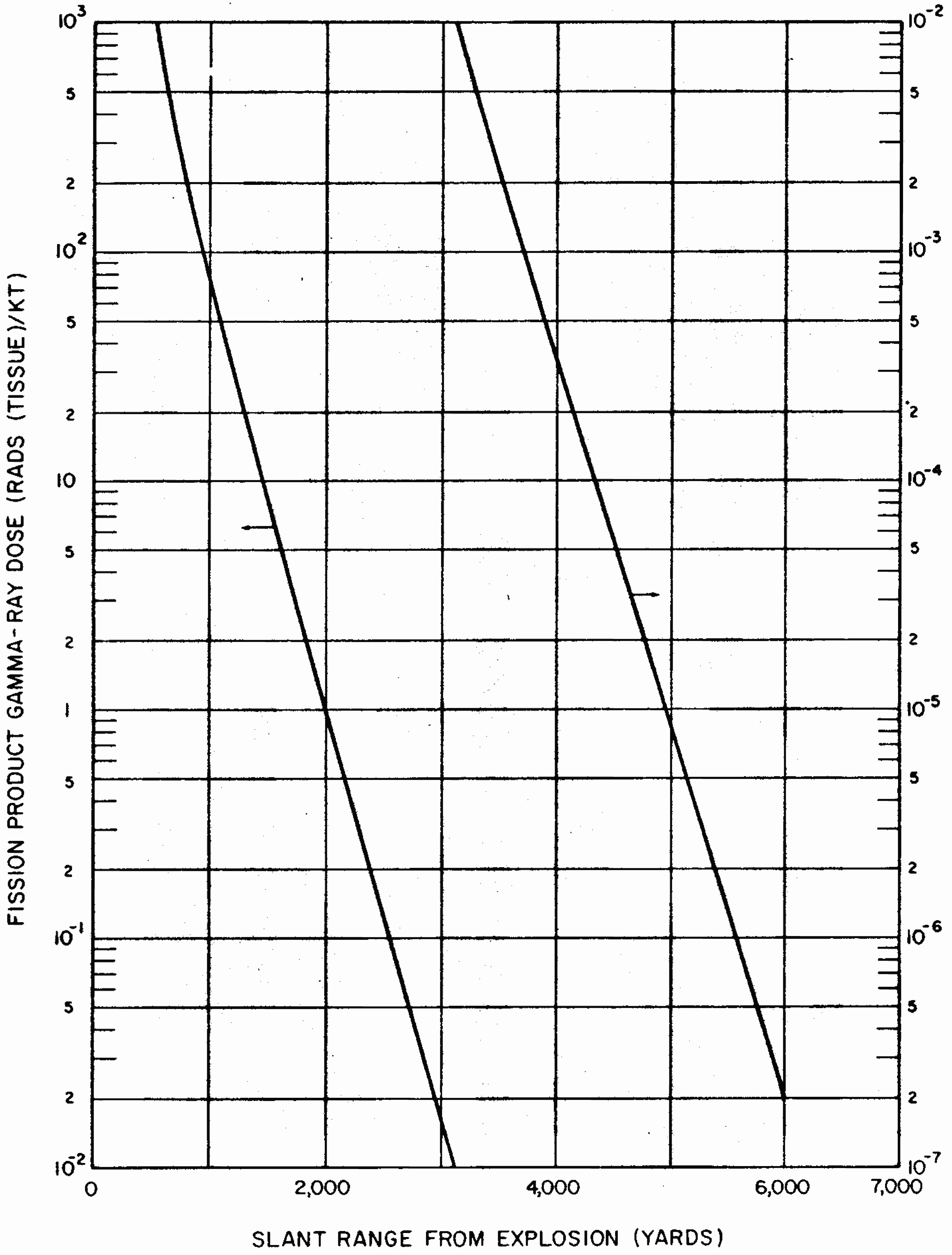
8.131 For thermonuclear weapons, the dose for a given distance as obtained from Fig. 8.130a must be multiplied by the fraction of the total yield that results from fission, e.g., 0.5 for a weapon with 50 percent fission yield, prior to multiplying by the effective yield as obtained from Fig. 8.130b. It should be noted that Fig. 8.130b is always entered with the total energy yield of the weapon to obtain the effective yield, since the cloud rise velocity and the hydrodynamic enhancement depend on the total energy release. Interpolation may be employed to obtain the effective yield for slant ranges that are not shown. The curves in Fig. 8.130b were calculated for a scaled height of burst of 200 W0.4 feet, where W is the total weapon energy yield in kilotons. For a given slant range the curve is terminated at the yield at which the height of burst is equal to that slant range.
8.132 The data for the effective yields in Fig. 8.132 are similar to those in Fig. 8.130b but are applicable to contact surface bursts. There is no simple method to interpolate or extrapolate these curves for fission-product gamma rays to other heights of burst; however, Fig. 8.130b may be taken to be reasonably accurate for most low air bursts, and Fig. 8.132 may be applied to near surface as well as to contact surface bursts. The results presented in Fig. 8.33a are based on the upper curves in Fig. 8.127a (for secondary gamma rays) and the curves in Figs. 8.130a and b. The results in Fig. 8.33b are based correspondingly on the curves in Fig. 8.127b and those in Figs. 8.130a and b.
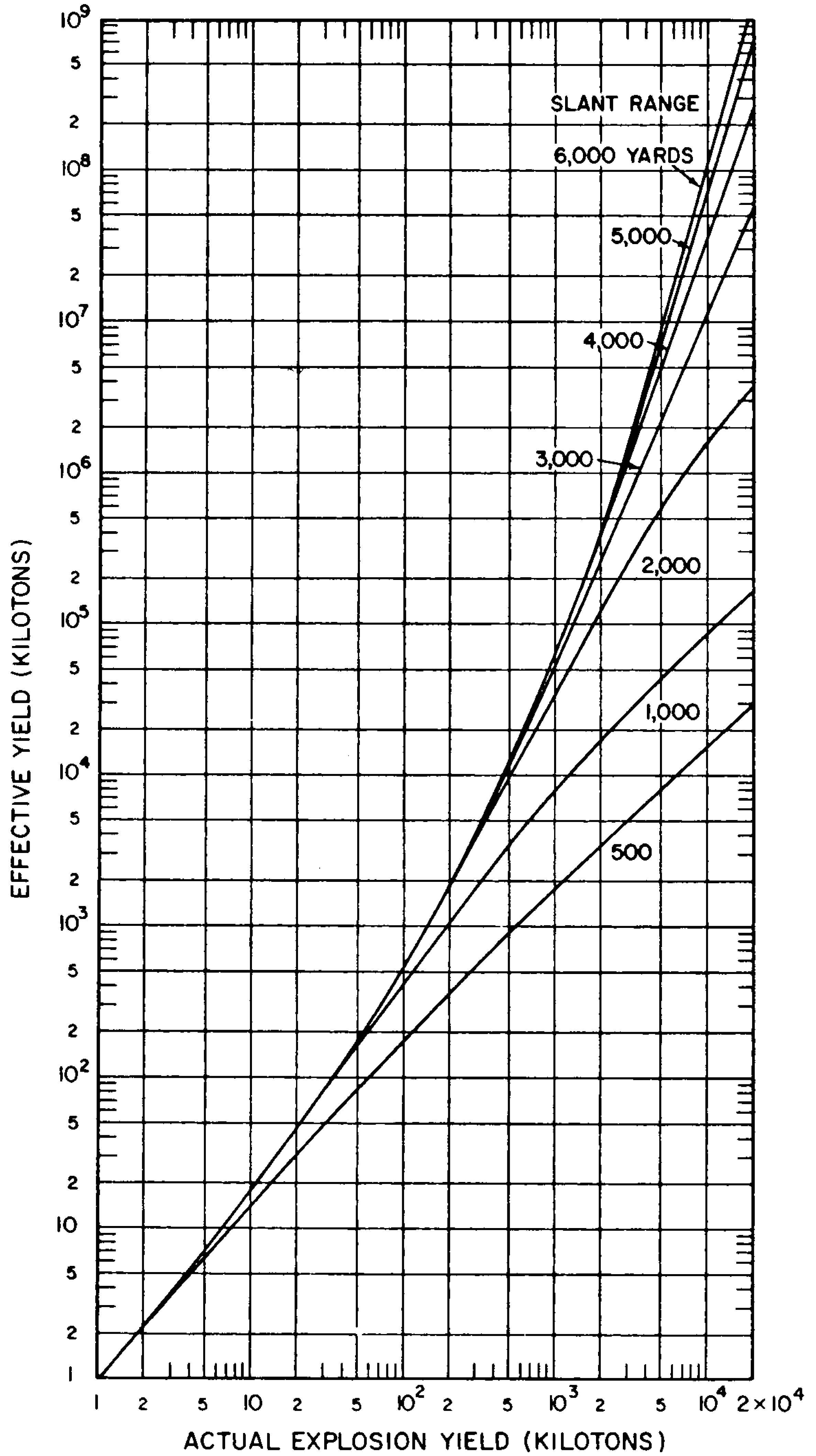
MECHANISMS IN TREE: IONIZATION
8.133 Two basic interactions of nuclear radiation with matter are important in connection with the transient-radiation effects on electronics (TREE); they are ionization and atomic displacement (§ 8.76). The charged particles. i.e., electrons and ions, produced by ionization eventually combine but the accompanying changes in materials may be more or less permanent. Some aspects of TREE depend on the relative durations of the radiation pulse and the recovery time. If the pulse duration is the longer, the effect is observed promptly. The magnitude of the effect is usually a function of the density of charged particles created by ionization and this is determined by the rate of energy absorption, i.e., by the dose rate. On the other hand, if the pulse length is short relative to the recovery time, the effect will be delayed. The amount of damage is then usually a function of the total energy absorbed, i.e., the dose. Thus, both absorbed dose and dose rate must be considered in assessing the effects of nuclear radiation on electronics; in many cases, the dose rate is the determining factor. The persistence of the effect is related, in general, to the recovery time.
8.134 The chief manifestations of ionization include (1) charge transfers, (2) bulk conductivity increase, (3) excess minority-carrier generation, (4) charge trapping, and (5) chemical change. These effects will be examined in turn in the following paragraphs.
8.135 Charge transfer results from the escape of some electrons produced by ionization from the surface of the ionized material. If the net flow of these electrons is from the ionized material to an adjacent material, the former will acquire a positive charge and the latter a negative charge. Consequently, a difference of potential will exist between the two materials. The most obvious effect of this potential difference is a flow of current through an electrical circuit connecting the two materials, and this current will produce electric and magnetic fields. If there is matter in the space between the two materials, the charge transfer may cause ionization and hence conduction if there are local electric fields. Finally, if the charge either originates or embeds itself in an insulator, a long-lived local space charge may result. The effects of charge transfer may thus be temporary or semipermanent.
8.136 The free charge carriers produced during ionization respond to an applied electric field by causing a net drift current; there is consequently a transient increase in conductivity. This effect is particularly important for capacitors, since the ability to retain or restore electrical charge is dependent on the low conductivity of the dielectric. In an ionizing environment the increase in the bulk conductivity results in a decrease of the stored charge in a capacitor.
8.137 In semiconductor devices, such as transistors and diodes, there are both positive (holes) and negative (electron) charge carriers, either of which may be in the minority. The effect of ionization in producing additional minority carriers is of prime concern in many semiconductors and is usually the most important manifestation of ionization in TREE. Some of the characteristics of semiconductor devices depend upon the instantaneous concentration of minority carriers in various regions of the device. Since ionizing radiation creates large (and equal) numbers of positive and negative charge carriers, there is a large relative increase in the concentration of minority carriers. The electrical operation of the device may thus be seriously affected. The current pulse observed in a semiconductor detector (§ 8.22) when exposed to radiation is an example of the effect of excess minority carriers, although in this case it is turned to advantage.
8.138 When free charge carriers are created in insulating materials and are trapped at impurity sites, sometimes present in such materials, many may not undergo recombination with the oppositely charged carriers, which may be trapped elsewhere. In these cases, the properties of the material may be altered semipermanently, even though there is no net charge in the material. This ionization effect is known as charge trapping. Trapped charge can change the optical properties of some substances, e.g., F (color) centers in alkali halides and coloration of glasses. The trapped carriers may be released thermally, either at the temperature of irradiation or by increasing the temperature. In either case, the resultant creation of free carriers is manifested by an increase in conductivity and sometimes by the emission of light (§ 8.24).
8.139 As a result of the recombination of electrical charges, sufficient energy may be released to disrupt chemical bonds. The material may thus suffer a chemical change which persists long after the charged particles have disappeared. This chemical change may be accompanied by permanent changes in the electrical and other properties of the material. However, the radiation dose required to produce a significant chemical effect is larger than would normally be encountered at a distance from a nuclear explosion where the equipment would survive blast and fire damage.
MECHANISMS IN TREE: ATOMIC DISPLACEMENT
8.140 Another potential damage mechanism of nuclear radiation in electronic systems involves the movement of electrically neutral atoms. Such displacement of atoms from their usual sites in a crystal lattice produces lattice defects. A common type of defect arises from the displacement of an atom from a normal lattice position to an “interstitial” position between two occupied normal positions. The displaced atom leaves behind an unoccupied normal lattice position (or “vacancy”), possibly some distance away. At least part of the damage to a crystalline material caused in this manner is permanent. Since many electronic devices contain crystalline semiconductor materials, usually silicon or germanium, displacement damage is of special concern for TREE.
8.141 Fast neutrons, in particular, are very effective in causing atomic displacement. The total number of defects (temporary and permanent) generated by a neutron depends on its energy. Thus, a 14-MeV neutron (from a thermonuclear weapon) produces about 2.5 times as many defects as a 1-MeV neutron (roughly the average energy from a fission weapon). For neutrons of a given energy (or energy spectrum) the number of defects is determined by the neutron fluence, and the changes in the properties of a semiconductor material are directly related to the total number of defects. Thus, the neutron fluence is an important consideration in assessing damage to a semiconductor caused by atomic displacement.
8.142 Some of the defects produced by the displacement process are permanent but others are temporary. The temporary defects are annihilated by re combination of the vacancy-interstitial pairs, i.e., by the movement of an interstitial atom into a vacancy, by combination with pre-existing lattice defects, or they may eventually escape from a free surface of the material The gradual disappearance of some defects is called “annealing” and the rate of annealing can be increased by raising the temperature. The degree of displacement damage in a crystalline semiconductor increases rapidly with time, reaches a peak, and then decreases as annealing becomes increasingly effective. The annealing process may lead to either an improvement or further degradation of the irradiated material, because in some cases thermally stable defects may result. These defects may be more or less effective than the unstable ones in changing a particular property.
8.143 Annealing processes fall roughly into two time frames. Rapid (or short-term) annealing occurs in hundredths of a second, whereas long-term annealing continues for times of the order of tens of seconds. At ambient temperature, annealing of temporary damage will be essentially complete within about half an hour. The ratio of the damage observed at early times (number of defects present) to the damage remaining after a long time is called the “annealing factor”; it depends on the observation time as well as on the temperature and the electrical condition of the material. The maximum number of defects created at early times following a fast-neutron burst is frequently important to the performance of electronics systems. The maximum annealing factor of a component indicates the peak damage that must be tolerated above the permanent damage if that component is to continue to function.
8.144 The lattice damage caused by atomic displacement degrades the electrical characteristics of semiconductors by increasing the number of centers for trapping, scattering, and recombination of charge carriers. The increase in trapping centers results in removal of charge carriers and thereby decreases the current flow. The additional scattering centers reduce the capability of the charge carriers to move through the semiconductor material. Finally, the additional recombination centers decrease the time during which the minority charge carriers are available for electrical conduction. The last effect, i.e., the reduced lifetime of the minority carriers, is the most important factor in determining the performance of a semiconductor device in an environment of radiation that can cause atomic displacement. The minority carrier lifetime is very roughly inversely proportional to the neutron fluence at large values of the fluence that are likely to cause damage to semiconductors. At sufficiently large fluences, the lifetime becomes too short for the semiconductor device to function properly.
BIBLIOGRAPHY
- , “Shielding Against Initial Radiations from Nuclear Explosions,” Oak Ridge National Laboratory, July 1973, ORNL RSIC-36.
- , “Nuclear Weapons Free Field Environment Recommended for Initial Radiation Shielding Calculations,” Oak Ridge National Laboratory, February 1972, ORNL TM-3396. “Basic Radiation Protection Criteria,” NCRP Report No. 39, National Council on Radiation Protection, Washington, D.C., 1971.
- , “Nuclear Engineering Handbook,” McGraw-Hill Book Co., Inc., 1958.
- , “A First-Last Collision Model of the Air/Ground Interface Effects on Fast-Neutron Distributions,” Nuclear Sci. and Eng., 19, 151 (1964).
- , “Initial Radiation Exposure from Nuclear Weapons,” Radiation Research Associates, Fort Worth, Texas, July 1972, RRA-T7201.
- , “Measured Low-Altitude Neutron and Gamma Dose Distributions Due to a 14- MeV Neutron Source,” E.G., and G., Inc., Las Vegas, Nevada, 1969, EGG 1183-1449.
- , “Measured High-Altitude Neutron and Gamma Dose Distributions Due to a 14- MeV Neutron Source,” E. G., and G., Inc., Las Vegas, Nevada, 1969, EGG 1183-1438.
- , “The Analysis of Radiation Effects in Semiconductor Junction Devices,” Sandia Corporation, Albuquerque, New Mexico, July 1967, SC-R-67-1158.
- , “Transmission of Photons Through Common Shield ing Media,” Oak Ridge National Laboratory, October 1974, ORNL-TM-4728.
- , “Neutron Transport in Non-Uniform Air by Monte Carlo Calculations, Volume I,” Kaman Nuclear, Colorado Springs, Colorado, January 1969, DASA 2236-I, KN-774-69-1.
- , “Protection from Penetrating Radiation of Nuclear Explosions,” English translation, Joint Publications Research Service, U.S. Department of Commerce, July 1971, JPRS 53498.
- , “The Effects of Cut-Off Energy on Monte Carlo Calculated Gamma-Ray Dose Rates in Air,” Radiation Research Associates, Fort Worth, Texas, 1966, RRA-M67.
- , “Calculations of Weapon Radiation Doses in Single-Compartment Above Ground Concrete Structures,” Radiation Research Associates, Fort Worth, Texas, November 1969, RRA-M93.
- National Bureau of Standards, “Measurement of Absorbed Dose of Neutrons and Mixtures of Neutrons and Gamma Rays,” NCRP Report No. 25, U.S. Government Printing Office, 1961, National Bureau of Standards Handbook 75.
- ”Protection Against Neutron Radiation,” NCRP Report No. 38, National Council on Radiation Protection, Washington, D. C., 1971.
- ”Radiation Damage and Defects in Semiconductors,” Conference Series, No. 16, July 1972. The Institute of Physics (London), 1973.
- ”Recommended Techniques for the Measurement of Selected Nuclear Radiation Effects on Electronic Components,” IBM Electronics Systems Center, Owego, New York, August 1967, DASA 627, Vol. II.
- , “Reactor Shielding for Nuclear Engineers,” U.S. AEC Report TID-25951, 1973.
- , “Time-Dependent Neutron and Secondary Gamma-Ray Transport in an Air-Over-Ground Geometry, Volume II. Tabulated Data,” Oak Ridge National Laboratory, September 1968, ORNL 4289.
- , “Status of Neutron Transport in the Atmosphere,” Oak Ridge National Laboratory, July 1970, ORNL-TM-3065.
- , “Radiation Effects in Semiconductors,” Proceedings of the Santa Fe Conference on Radiation Effects in Semiconductors, Plenum Press, 1968.
ENDNOTES
- 1 The term “scattering” (cf. § 7.10) is used because, after interacting with the nucleus, the neutron of lower energy generally moves off in a direction different from that in which the original neutron was traveling before the collision. [ref. § 8.09] X
- 2 In an isomer of a particular nuclear species the nuclei are in a high-energy (or excited) state with an appreciable half-life. The isomers of interest here are those that decay rapidly, with a half-life of about one thousandth of a second or less, by the emission of the excess (or excitation) energy as gamma radiation. [ref. § 8.10] X
- 3 According lo the official definition, 1 roentgen produces electrons (in ion pairs) with a total charge of 2.58 × 10-4 coulomb in 1 kilogram of dry air. [ref. § 8.17] X
- 4 The rough equivalence between a gamma (or X-ray) exposure of 1 roentgen and the absorption in body tissue of 1 rad holds for photons of intermediate energies (0.3 lo 3 MeV). For photon energies outside the range from 0.3 to 3 MeV, the exposure in roentgens is no longer simply related to the absorption in rads. [ref. § 8.18] X
- 5 The density referred to here (and subsequently) is that of the air before it is disturbed by the explosion (cf. § 8.36). [ref. § 8.33] X
- 6 The “half-value thickness” is sometimes used; it is defined as the thickness of a given material which reduces the dose of impinging radiation to (approximately) one half. Two such thicknesses decrease the dose to one fourth; three thicknesses to one eighth, etc. [ref. § 8.39] X
- 7 The tenth-value thicknesses are for gamma rays that are incident perpendicularly on the slab of material. If the rays make an angle θ with the perpendicular, the tenth-value thickness is obtained approximately by multiplying the values in the table by cosine θ, provided θ is less than 45°. [ref. § 8.41] X
- 8 The ionization and excitation resulting from the interaction of fast neutrons with hydrogen in tissue is considered to be the main cause of biological injury by neutrons. [ref. § 8.58] X
- 9 The neutron fluence (at a given energy) is, in a sense, a measure of the neutron exposure (at that energy). The absorbed dose can be derived from the fluence by allowing for the energy deposited by the neutrons in a specified material. [ref. § 8.61] X
- 10 For the dependence of neutron fluences at various energies on the energy yield and distance from a nuclear explosion, see Figs. 8.117a and b. [ref. § 8.79] X
- 11 In this and other cases, the damage is determined by the dose rate (rather than the dose) of gamma radiation. [ref. § 8.84] X
- 12 The remaining sections of this chapter may be omitted without loss of continuity. [ref. Section 5] X
- 13 In this equation, the intensity is the number of (uncollided) photons per square centimeter per second. A similar equation, with the “linear energy absorption coefficient” replacing the linear attenuation coefficient, is applicable when the intensity is expressed in terms of the total energy of the photons per square centimeter per second. [ref. § 8.95] X
- 14 A relaxation length may be taken as the distance in which the radiation intensity in a specified material is decreased by a factor of e, where e is the base of the natural logarithms (about 2.718). The relaxation length in a given material depends on the neutron energy and on whether the direct fluence only or the total (direct plus scattered) fluence is being considered. [ref. § 8.120] X
- 15 It should be noted that the ordinates in Fig. 8.14 are the energy emission rates; the total energy would then be obtained by integration over the effective emission time. This time is very much shorter for isomeric decay gamma rays than for fission products. [ref. § 8.125] X