Chapter X RADIO AND RADAR EFFECTS
INTRODUCTION
RADIO BLACKOUT
10.01 The transmission of electromagnetic waves with wavelengths of 1 millimeter or more, which are used for radio communications and for radar, is often dependent upon the electrical properties, i.e., the ionization(§ 8.17), of the atmosphere. The radiations from the fireball of a nuclear explosion and from the radioactive debris can produce marked changes in the atmospheric ionization. The explosion can, therefore, disturb the propagation of the electromagnetic waves mentioned above. Apart from the energy yield of the explosion, the effects are dependent on the altitudes of the burst and of the debris and on the wavelength (or frequency) of the electromagnetic waves. In certain circumstances, e.g., short-wave (high frequency) communications after the explosion of a nuclear weapon at an altitude above about 40 miles, the electromagnetic signals may be completely disrupted, i.e., “blacked out,” for several hours.
10.02 In this chapter, the normal ionization of the atmosphere will be described and this will be followed by a discussion of the disturbances produced by nuclear bursts at various altitudes. Consideration will then be given to the effects of these disturbances on the propagation of electromagnetic waves in different frequency ranges. Apart from the effects that can be ascribed directly to changes in ionization, radio communications and radar signals can be degraded in other ways, e.g., by noise, distortion, changes in direction, etc. These disturbances, which cannot be treated in a quantitative manner, will be discussed briefly.
ELECTROMAGNETIC PULSE
10.03 Another consequence of a nuclear explosion that may cause temporary interference with radio and radar signals is an electrical (or electromagnetic) pulse of short duration emitted from the region of the burst. The most serious potential effects of this pulse are damage to electrical and electronic equipment, rather than to the propagation of electromagnetic waves. Hence, the electromagnetic pulse will be considered separately in Chapter XI.
ATMOSPHERIC IONIZATION PHENOMENA
EFFECT OF IONIZATION ON ELECTROMAGNETIC WAVES
10.04 Ionization, that is, the formation of ion pairs consisting of separated electrons and positive ions, can be produced, either directly or indirectly, by the gamma rays and neutrons of the prompt nuclear radiation, by the beta particles and gamma rays of the residual nuclear radiation, by the X rays and the ultraviolet light present in the primary thermal radiation, and by positive ions in the weapon debris. Hence, after a nuclear explosion, the density of electrons in the atmosphere in the vicinity is greatly increased. These electrons can affect electromagnetic (radio and radar) signals in at least two ways. First, under suitable conditions, they can remove energy from the wave and thus attenuate the signal; second, a wave front traveling from one region into another in which the electron density is different will be refracted, i.e., its direction of propagation will be changed. It is evident, therefore, that the ionized regions of the atmosphere created by a nuclear explosion can influence the behavior of communications or radar signals whose transmission paths encounter these regions.
10.05 When an electromagnetic wave1 interacts with free electrons, some of the energy of the wave is transferred to the electrons as energy of vibration. If the electrons do not lose this energy as the result of collisions with other particles (atoms, molecules, or ions) in the air, they will reradiate electromagnetic energy of the same frequency, but with a slight time delay. Thus, the energy is restored to the wave without loss, but with a change in phase (§ 10.82 et seq.). If, however, the air density is appreciable, e.g., more than about one ten-thousandth (10-4) of the sea-level value, as it is below about 40 miles altitude, collisions of electrons with neutral particles will take place at a significant rate. Even above 40 miles, collisions between electrons and ions are significant if the electron density is abnormally high. In such collisions, most of the excess (coherent) energy of the electron is transformed into kinetic energy of random motion and cannot be reradiated. The result is that energy is absorbed from the wave and the electromagnetic signal is attenuated.
10.06 Other conditions being the same, more energy is absorbed from an electromagnetic wave by an ionized gas as the wavelength of the signal is increased, i.e., as its frequency decreases. This may be regarded as being due to the longer time interval, as the frequency is decreased, between successive alterations (or reversal6) of the oscillating electromagnetic field (§ 1.73). When the accelerating influence of the wave is applied for a longer time, a given electron will attain a higher vibrational velocity during each cycle of the wave, and will dissipate a greater amount of energy upon collision.
10.07 Positive and negative ions can also absorb energy from an electromagnetic wave. Because of their larger mass, however, the ions attain much lower velocities than electrons and so they are less effective in absorbing energy. Thus, the effects of ions may ordinarily be neglected. However, for some situations in the denser (low altitude) portion of the atmosphere, where ions can persist for an appreciable time, or for frequencies low enough for the ions to have time to acquire significant velocity before reversal of the electromagnetic field, the effect of ions may be important.
10.08 A radio or radar wave traveling upward from the ground begins to be bent (refracted) when an increase of electron density is encountered. Increased electron density causes the wave path to bend away from the region of higher electron density toward the region of lower density (§ 10.85). As the electromagnetic wave penetrates farther into a region where the electron density increases toward a peak value, more and more bending occurs. For certain combinations of the angle of incidence (angle between propagation direction and the vertical), the electron density, and the frequency, the wave may actually be refracted back toward the earth (Fig. 10.08). This process is commonly referred to as “reflection,” although it is not the same as true reflection, in which there would be no penetration of the ionized layer of air. True (or specular) reflection, as from a mirror, does occur to some extent especially with electromagnetic waves of the lowest radio frequencies.

IONIZATION IN THE NORMAL ATMOSPHERE
10.09 In order to understand the effects of free electrons on radio and radar systems, it is necessary to review briefly the ionization in the normal, undisturbed atmosphere. Below an altitude of about 30 miles, there is little ionization, but above this level there is a region called the “ionosphere,” in which the density of free electrons (and ions) is appreciable (see Fig. 9.126). The ionosphere consists of three, more-or-less distinct, layers, called the D-, E-, and F-regions. Multiple layers, which sometimes occur in the E- and F regions, may be disregarded for the present purpose. Typical variations of electron density with altitude and with time of day are illustrated in Fig. 10.09. The approximate altitudes of the three main regions of the ionosphere are given in Table 10.09.

| Region | Approximate Altitude (miles) |
|---|---|
| D | 30-55 |
| E | 55-95 |
| F | Above 95 |
10.10 Although the D-, E-, and F regions always exist in the daytime and the E- and F-regions at night, the details of the dependence of the electron density on altitude, especially in the F region, vary with the season, with the geographic latitude, with the solar (sun spot) activity, and with other factors. The curves in Fig. 10.09 are applicable to summer, at middle latitudes, around the time of maximum sunspot activity. The effects of the variable factors mentioned above are fairly well known, so that the corresponding changes in the electron density-altitude curve can be predicted reasonably accurately.
10.11 In addition to these systematic variations in the electron density, there are temporary changes arising from special circumstances, such as solar flares and magnetic storms. Solar flares can cause a ten-fold increase in the electron density in the D-region, but that in the F-region generally increases by no more than a factor of two. Magnetic storms, on the other hand, produce most of their effect in the F-region. In some latitudes, the maximum electron density in the ionosphere during a magnetic storm may decrease to some 6 to 10 percent of its normal value.
10.12 Apart from these major changes in electron density:, the causes of which are known, there are other variations that are not well understood. Sometimes an irregular and rapidly varying increase in the electron density is observed in the E-region. Apparently one or more layers of high electron density are formed and they extend over distances of several hundred miles. This is referred to as the “sporadic-E” phenomenon. A somewhat similar effect, called “spread-F,” in which there are rapid changes of electron density in space and time, occurs in the F-region. The areas affected by spread-F are generally much smaller than those associated with sporadic-E.
CHARACTERISTICS OF THE IONOSPHERE
10.13 The composition of the atmosphere, especially at the higher altitudes, varies with the time of day and with the degree of solar activity; however, a general description that is applicable to daytime conditions and mean sunspot activity is sufficient for the present purpose. Near the earth's surface, the principal constituents of the atmosphere are molecular nitrogen (N2) and molecular oxygen (O2). These diatomic gases continue to be the dominant ones up to an altitude of approximately 75 miles. At about 55 miles, ultraviolet radiation from the sun begins to dissociate the oxygen molecules into two atoms of oxygen (O). The extent of dissociation increases with altitude, so that above 120 miles or so, oxygen atoms are the dominant species in the low-pressure atmosphere. This condition persists up to an altitude of some 600 miles. Ozone (O3) and nitric oxide (NO) are formed in the lower atmosphere by the action of solar radiations on the oxygen and nitrogen. Although the amounts of ozone and nitric oxide are quite small, they are important because each absorbs radiation and enters into chemical reactions in a characteristic manner.
10.14 The electrons (and positive ions) in the normal ionosphere are produced by the interactions of solar radiations of short wavelength with the various molecular and atomic species present in the atmosphere. In the D region, the ions are almost exclusively NO+, and these ions are also the most important in the E-region; in the latter region, however, there are, in addition, about one-third as many $\text{O}^+_2$ ions. Atomic oxygen ions, O+, begin to appear in the upper parts of the E-region, and their proportion increases with altitude. In the F-region, the proportion of NO+ and $\text{O}^+_2$ ions decreases, whereas that of O+ increases steadily. Above an altitude of about 120 miles (up to 600 miles), O+ ions are dominant.
10.15 The actual electron density at any altitude depends on the rate of formation of electrons as a result of ionization and their rate of removal, either by recombination with positive ions or by attachment to neutral particles (molecules or atoms). Recombination tends to be the more important removal process at high altitudes (low atmospheric pressure), whereas attachment to neutral particles predominates at lower altitudes, where molecular nitrogen and oxygen are the main components of the atmosphere.
10.16 At altitudes below about 30 miles, i.e., below the D-region, where the air is relatively dense, the probability of interaction between free electrons and neutral molecules is large. The few electrons that are produced by short wavelength solar radiation that penetrates so low into the atmosphere are thus rapidly removed by attachment. The density of free electrons in the atmosphere below about 30 miles is consequently so small that it can be neglected.
10.17 In the altitude range from roughly 30 to 55 miles (D-region of the ionosphere), the density of neutral particles is relatively low, between about 10-3 and 10-5 of the sea-level density. Because of this low density, the rate of attachment is not large and electrons remain free for several minutes. The average lifetime varies with location and the time of the year, but it is long enough for the radiation from the sun to maintain a peak density between about 102 and 103 electrons per cubic centimeter (electrons/cm3) in the daytime. At night, when electrons are no longer being generated by solar radiations, the free electrons in the D-region disappear. Although the density of neutral particles is small enough to permit the electrons (in the daytime) to have an appreciable average life, it is nevertheless sufficiently large for collisions to cause considerable attenuation of electromagnetic waves, in the manner described in § 10.05.
10.18 In the E-region of the ionosphere (55 to 95 miles altitude), the air density is quite low, about 10-5 to 10-8 of the sea-level value, and the average lifetime of electrons is even longer than in the D-region. The daytime electron density is about 103 to 105 electrons/cm but most of the ionization, as in the D-region, disappears at night. However, because of the very low density of neutral particles, the frequency of collisions between them and electrons is so small that there is relatively little attenuation of electromagnetic signals in the E-region. If sporadic-E conditions exist, radio signals are reflected (§ 10.08) in an erratic manner.
10.19 The F-region extends upward from an altitude of about 95 miles. Here the neutral-particle density is so low that free electrons have extremely long life times. At about 190 miles, the peak electron density in the daytime is approximately 106 electrons/cm3, decreasing to about 105 electrons/cm3 at night. During the day there are various layers of ionization in the F-region, which tend to merge and lose their identity at night. The altitude of peak ionization may also shift at night. Other factors causing changes in the F-region were referred to earlier (§ 10.12). Attenuation of electromagnetic signals in the F-region is small, despite the high electron density, because of the very low electron-neutron collision frequency; however, reflection effects (§ 10.08) make the region important.
10.20 Normally, the low electron densities in the D-region are sufficient to reflect back to earth only those electromagnetic waves with frequencies below about 1 million hertz, i.e., 1 megahertz (§ 1.74), provided the angle of incidence is small. At larger angles, the limiting frequency for reflection by the normal D-region is increasingly less than 1 megahertz. Waves of higher frequency pass through the D-region, with some refraction (bending) and attenuation, and penetrate into the E-region or into the F-region if the frequencies are high enough. Reflection may then occur in the E- or F-region, where the electron densities are higher than in the D region. For a given angle of incidence, the electron density required for reflection increases with the frequency of the electromagnetic wave. The smaller the angle of incidence, i.e., the more nearly vertical the direction of propagation, the higher the frequency that will be reflected by a given electron density.
IONIZATION PRODUCED BY NUCLEAR EXPLOSIONS
INTRODUCTION
10.21 Up to three-fourths of the energy yield of a nuclear explosion may be expended in ionizing the atmosphere. The resulting changes are characteristic of the given weapon and of the burst and debris altitudes. The ionization effects caused by the nuclear and thermal radiations from a low-altitude nuclear explosion are much more intense within a limited volume of space, i.e., in and near the fireball, than the changes produced naturally, e.g., by solar flares. Nuclear explosions at high altitudes may affect a considerable portion of the ionosphere in ways somewhat similar to changes in solar activity; however, the mechanisms and details of the interactions with the atmosphere are quite different. Because of the complexities of these interactions, descriptions of “typical” changes to be expected from a nuclear explosion are often not applicable or even very meaningful. A careful analysis of each situation, with the conditions stated fairly explicitly, is usually necessary.
10.22 Atmospheric ionization and disturbances to the propagation of electromagnetic signals caused by a nuclear explosion can be described in terms of four spatial regions: (1) the hot fireball, (2) the atmosphere surrounding the fire ball, (3) the D-region, and (4) the high altitude region which includes the normal E- and F-regions of the ionosphere.
10.23 Fireballs from explosions at low altitude are relatively small (roughly, a 1-megaton explosion at sea level produces a fireball of about 0.6 mile diameter at 1 second). The air inside the fireball is at a temperature of many thousands of degrees. Electron density and collision frequency are high, and the absorption of electromagnetic waves is so large that the fireball is considered to be opaque. At intermediate burst altitudes (up to about 50 or 60 miles), the early fireball is larger in size, but it is still defined as a hot, ionized mass of air which is opaque to radio and radar signals for many seconds With increasing altitude the characteristics of the region of energy absorption change. At burst altitudes above about 190 miles, the atmosphere is very thin and the energy from the nuclear explosion can spread over very large distances.
10.24 When the burst point is below the D-region, the atmosphere around the fireball is ionized in varying degrees by the initial thermal and nuclear radiations and by the delayed gamma rays and beta particles from the radioactive debris. The chemistry of the atmosphere may be modified significantly, thus making predictions of electron persistence difficult (and greatly complicating the problem of analyzing multiple-burst situations). For near-surface explosions, the density of the air prevents radiation from escaping very far from the fireball, and the ionization is both localized and short-lived due to very rapid attachment of free electrons to neutral particles. As the detonation altitude is increased the radiation can escape to greater distances, and the electron density will reach values at which electromagnetic signal propagation can be affected.
10.25 When prompt or delayed radiation from the explosion can reach the D-region, the electron density of that region is enhanced. Most of the widespread and persistent absorption of electromagnetic waves then takes place in and near the D-region of the normal ionosphere. For electromagnetic waves in the radio and radar frequency ranges, circumstances are such that the maximum attenuation usually occurs within a layer 10 miles deep centered at an altitude of about 40 miles (§ 10.128). Hence, most of the subsequent discussion pertaining to D-region ionization will be in terms of the free electron density at an altitude of 40 miles.
10.26 In the E- and F-regions of the ionosphere, the frequency of electron neutral particle collisions is low, and refraction rather than absorption is generally the predominant effect. When the burst or debris altitude is high enough for prompt or delayed radiation to reach the E- and F-regions, the electron density of those regions may be increased. On the other hand, nuclear explosions sometimes cause a decrease of electron density in the E- and F-regions, largely due to traveling hydrodynamic and hydromagnetic disturbances2 and to changes in air chemistry (§ 10.71 et seq.).
10.27 Increased ionization in the D-region may occur not only in the vicinity of the nuclear explosion, but also at its magnetic conjugate in the earth's opposite hemisphere (§ 2.143). Charged particles, especially beta particles (electrons), resulting from the explosion will spiral along the earth's magnetic field line:;. Upon reaching the conjugate region, the beta particles will cause ionization similar to that produced near the burst point.
ENERGY DEPOSITION
10.28 A detailed analysis of energy deposition, the starting point for examining the effects of nuclear explosions on the propagation of radio and radar signals, is very complicated. The fundamental principles, however, are well known and relatively simple. Consider ionizing radiation entering the earth's atmosphere from a nuclear explosion at high altitude or, as it normally does, from the sun. As it travels downward, the radiation at first encounters air of such low density that very few interactions occur with atmospheric atoms and molecules. Hence, very little ionization is produced. As the air density increases with decreasing altitude, interactions of the atoms and molecules with the radiation take place at rapidly increasing rates and energy is removed from the radiation.
10.29 The concept of “stopping altitude” provides a useful approximate model for treating the interaction of ionizing radiation and the atmosphere in which the density changes with altitude. The stopping altitude for a given type of radiation is the level in the atmosphere to which that radiation coming from above will penetrate before losing so much of its energy that it produces little further ionization. The radiation is then said to have been “stopped.” Most of the energy will actually be deposited within a few miles of the stopping altitude. Only a small proportion of the energy is absorbed at the higher altitudes where the air has a lower density and is relatively transparent to the radiation, and little energy remains to be given up at lower altitudes. Different types of radiation deposit their energy in the atmosphere in different ways and thus have different stopping altitudes. Table 10.29 shows approximate stopping altitudes for various ionizing outputs from a typical nuclear explosion. The altitude quoted for debris ions refers to ionization that results from the random (thermal) motion of these ions. The debris mass can, however, be carried to greater heights by the rising fireball and cause ionization by the emission of delayed radiations.
| Weapon Output | Stopping Altitude (miles) |
|---|---|
| Prompt radiation | |
| X rays | 35 to 55 |
| Neutrons and gamma rays | 15 |
| Debris ions | 70 |
| Delayed radiation | |
| Gamma rays | 15 |
| Beta particles | 35 |
10.30 For detonations below 15 miles altitude, the minimum stopping altitude in Table 10.29, the air is essentially opaque to all ionizing radiations. The radiation will penetrate only a fairly short distance into the atmosphere before most of its energy is absorbed in causing ionization (or is transformed into other kinds of energy). As the altitude of the explosion increases to 15 miles and above, the radiation can escape to increasingly greater distances. Once the stopping altitude for a given ionizing radiation is reached, the atmosphere above the burst is relatively transparent to that radiation, which can then travel upward and outward to great distances.
10.31 Below the stopping altitude, in a region of uniform density, the nominal penetration distance of ionizing radiation of a particular kind and energy is inversely proportional to the air density. (The penetration distance is often expressed in terms of the mean free path, as described in § 2.113.) For a particular radiation of a single energy traveling through an undisturbed region of constant density, the penetration distance (or mean free path) can be calculated relatively easily. For a radiation spectrum covering a range of energies and for complex paths along which the air density changes, the computations are more laborious. For a disturbed atmosphere, calculations of the penetration distance are difficult and not very reliable.
LOCATION OF RESULTANT IONIZATION
10.32 The region of maximum energy deposition is the location where ion-pair production is the greatest, but it is not always the location of the maximum density of free electrons. At altitudes below about 30 miles, i.e., at relatively high air densities, removal processes are so rapid that the average lifetime of a free electron is a fraction of a second. An extremely high ion-pair production rate is then required to sustain even a few free electrons per cubic centimeter. But in the D-region (starting at about 30 miles altitude) removal processes are not so rapid and higher electron densities are possible. For the delayed gamma rays, for example, the stopping altitude, i.e., the region of maximum energy deposition and ion pair production rate, is 15 miles; however, the resultant electron density tends to a maximum at a higher altitude in the D-region.
10.33 To understand the ionization resulting from nuclear explosions, it is helpful to examine four detonation altitude regimes separately; they are: (1) below 10 miles, (2) between 10 and 40 miles, (3) between 40 and 65 miles, and (4) above 65 miles. Different mechanisms associated with various burst heights will be considered, but it should be understood that these altitude regimes are somewhat arbitrary and are chosen for convenience in bringing out the changes in behavior that occur with burst height. Actually, there are no lines of demarcation between the various altitude ranges; the changes are continuous, and one type of mechanism gradually supersedes another and becomes dominant. The four spatial regions where there may be significant effects (§ 10.22) also shift in importance as the altitudes of the detonation and of the radioactive debris change.
DETONATIONS BELOW 10 MILES ALTITUDE
10.34 For nuclear explosions at altitudes below 10 miles (and somewhat higher), most of the energy is deposited in the atmosphere in the immediate vicinity of the detonation, resulting in the formation of the fireball and the air blast wave, as described in Chapter II. The electron density within the fireball, initially at least equal to the particle density (about 1019/cm3), will remain above about 108 electrons/cm3 for times up to 3 and 4 minutes, depending on the nature of the weapon. For about 10 seconds the fireball temperature will be high enough (above 2,500° Kelvin) to cause significant ionization of the air by the thermal radiation (§ 10.04). After this period, beta radiation from the radioactive debris within the fireball may sustain the ionization level for up to 3 or 4 minutes. Thus, the fireball region will be sufficiently ionized to absorb electromagnetic signals for a period of at least 10 seconds and possible for as long as 3 or 4 minutes; however, the spatial extent of the ionization will be small.
10.35 The fireball will be spherical in shape initially. After a few seconds, as the hot fireball rises upward buoyantly (§ 2.129), it will take the form of a torus. The torus, having lost its luminous qualities, will coalesce into a flattened cloud shape. The transition from a fireball or torus to a debris cloud is indefinite, but at late enough times after a few minutes-the fireball as such will cease to exist, and only a cloud of radioactive debris will remain. This cloud will reach a final stabilization altitude in about 5 minutes. It will then be spread by whatever winds prevail at that altitude range. Typically, the average spreading velocity is about 35 feet per second.
10.36 The atmosphere surrounding the fireball will be ionized by prompt neutrons and by prompt gamma radiation, but the free electrons thus formed will persist less than a second. The air will also be ionized by the delayed radiation emitted continuously from the radioactive debris within the fireball. Close to the fireball, the continuous emission from the adjacent gamma-ray source will result in a high electron density in spite of the fairly rapid removal of electrons by attachment of air particles at the low altitudes under consideration. Thus, for detonations below 10 miles, there will be a region surrounding the fireball which will absorb electromagnetic waves appreciably for tens of seconds. This effect will be negligible for most radiofrequency systems, but it may be significant for radars with highly directional beams that pass fairly near (in addition to those passing through) the fireball.
10.37 In the atmosphere around the region referred to above, the electron density will be much lower because the gamma rays are somewhat attenuated by the air, and the electrons that are formed are removed rapidly by attachment. Hence, the number of free electrons is not expected to be as large, neither will they be as widely distributed, as in the region around the fireball for bursts at higher altitudes (§ 10.43 et seq.). Refraction of radar signals (§ 10.118) and clutter (§ 10.120) may then be more significant than absorption. These effects are also important if the signals pass through or near the stem or cloud of a burst that is sufficiently low for debris from the surface to be carried aloft.
10.38 The D-region is not affected to any great extent by prompt radiation from nuclear explosions below 10 miles, since the burst is below the stop ping altitude for X rays, neutrons, and gamma rays (Table 10.29). Ionization in the D-region may be increased, however, by delayed radiation, if the radioactive debris is carried upward by the rising fireball above 15 miles, the stopping altitude for gamma radiation. There may be additional ionization due to beta particles if the debris rises as high as 35 miles, but this is expected only for weapons of large yield (see Fig. 10.158c).
10.39 Ionization in the E- and F regions is not changed significantly by radiation from a nuclear explosion below 10 miles, except possibly by the rising debris from a high-yield burst (cf. § 10.41). However, perturbations in the refractive properties of the F-region have been noted following explosions in this altitude regime. Traveling disturbances (§ 10.26) that move outward in the E- and lower F-regions appear to result from the initial blast wave.
DETONATIONS AT 10 TO 40 MILES ALTITUDE
10.40 If the explosion occurs in the altitude regime of roughly 10 to 40 miles, thermal energy radiated as X rays will be deposited in the vicinity of the burst, as at lower altitudes, with subsequent reradiation to form the familiar fireball. Ionization by debris ions or by beta particles within the fireball may sustain the electron density after the temperature has fallen to the 2,500° Kelvin required for significant thermal ionization by air. The fireball region will be ionized to high levels-more than 107 electrons per cubic centimeter-for a period of at least 30 seconds and possibly for longer than 3 minutes. The spatial extent of the ionization will be larger than for detonations at the lower altitude considered previously.
10.41 The fireball will be spherical in shape initially, with the transition from sphere to torus occurring later than for bursts at lower altitudes. Furthermore, the debris, most of which is carried upward by the hot, rising fireball, may reach considerably greater heights. Multimegaton weapons detonated near the upper limit of the 10 to 40 miles altitude regime will begin to exhibit the effects of an initial ballistic impulse, caused by pressure gradients across the large vertical diameter of the fireball (§ 2.129). As the fireball and debris rise into thinner air, they continue to expand. The ballistically rising fireball can reach altitudes far above the detonation point. Because of the rapid upward motion of the fireball and the decrease in atmospheric density with altitude, the density of the fireball may be greater than that of the surrounding atmosphere. Overshoot then occurs, and after reaching maximum altitude, the fireball descends until it encounters air of density comparable to its own.
10.42 When the cloud of debris stabilizes in altitude, its horizontal spread will be influenced by diffusion and by the prevailing winds. A spreading velocity of 165 feet per second is a reasonable estimate for debris at altitudes between about 50 and 125 miles; the spread is, however, more complex than is implied by such an assumption of a uniform expansion.
10.43 For bursts in the 10 to 40 miles altitude regime, the X-rays are largely confined within the fireball, especially at the lower altitudes. Even though the prompt gamma rays carry only a small proportion of the explosion energy (§ 10.138), they will cause ionization in the surrounding air for a very short time. However, the main source of prompt ionization in the surrounding air (and also in the D-region for detonations above 15 miles) appears to be the fast neutrons. There are three important interaction processes of such neutrons with atomic nuclei in the atmosphere which can lead to ionization; they are absorption, inelastic scattering, and elastic scattering (see Chapter VIII). The amount of absorption is small for fast neutrons and the inelastic scattering gamma rays are spread over a large volume, so that the resulting electron density is low. Most of the neutron-induced (prompt) ionization arises from elastic scattering of the neutrons. The nuclei that recoil from the scattering process have sufficient energy to produce ionization by interaction with atmospheric atoms and molecules.
10.44 The persistent ionization in the air is caused mainly, however, by delayed gamma radiation. Most of the beta particles from the radioactive debris are absorbed within the fireball, but the gamma rays can travel great distances when the debris is above their stopping altitude (15 miles). The size of the ionized region surrounding the fire ball can then be quite large. Calculation of the electron densities is fairly complicated since it depends on the attenuation of the gamma rays by the atmosphere and the electron loss mechanisms which change with altitude.
10.45 Ionization in the D-region from delayed gamma rays and beta particles will be much more important for detonations in the 10 to 40 miles altitude regime than for those below 10 miles. If the debris attains an altitude above 15 miles, the delayed gamma rays can reach the D-region and produce ionization there. When the debris is below 35 miles, the stopping altitude for beta particles, the energy of these particles is deposited close to or within the debris cloud. The ionization is thus restricted to this region.
10.46 For the beta particles to cause ionization in the D-region, the debris must be above 35 miles. Because of their electric charge, the spread of the beta particles is largely prevented by the earth's magnetic (geomagnetic) field. The area over which the beta particles produce ionization in the D-region is thus essentially the same as the area of the debris when its initial expansion has ceased.
10.47 If the debris rises above 40 miles, the beta particles will travel back and forth along the geomagnetic field lines. They will then cause ionization in the local D-region and also in the magnetic conjugate region in the opposite hemisphere of the earth (Fig. 10.47). If the radioactive debris is uniformly distributed over a horizontal plane, the electron density in the D-region due to the beta particles will be about the same in both hemispheres. In practice, atmospheric winds and turbulence and geomagnetic anomalies cause the distribution of the debris to be nonuniform, but a uniform distribution is generally assumed for estimating electron densities resulting from nuclear explosions.

10.48 Unlike the beta particles, the gamma rays are not affected by the geomagnetic field and they can therefore spread in all directions. If the debris rises above 40 miles, the delayed gammas can produce ionization over a large area in the D-region. The ionization is not restricted by the tube of magnetic field lines containing the debris, as is that from the beta particles. The D-region ionization caused by the delayed gamma rays is this more extensive in area although usually less intense than that due to the beta particles.
10.49 Since the beta particles are largely prevented from spreading by the geomagnetic field, the ionization they produce (in the D-region) is not greatly affected by the altitude to which the radioactive debris rises, provided it is above 40 miles. For the accompanying gamma radiation, however, the intensity, and hence the associated ionization, decreases the higher the altitude of the debris above the D-region. The areal extent increases at the same time. Gamma-ray ionization in the magnetic conjugate region will be much smaller and will arise from such debris ions as have traveled along the geomagnetic field lines and reached the vicinity of the D-region in the other terrestrial hemisphere (§§ 2.141, 10.64).
10.50 There are two other sources of ionization in the conjugate region, namely, Compton electrons and neutrons. Gamma rays lose part of their energy in the atmosphere by Compton scattering (§ 8.89). If the Compton electrons are formed above about 40 miles, they will either deposit their energy (and cause ionization) locally in the D-region or be guided by the geomagnetic field to the conjugate region. Since delayed gamma rays are spread over a fairly large volume when the radioactive debris is above about 15 miles, Compton electrons can produce widespread ionization. The space affected is larger than that in which beta particles cause ionization in both conjugate regions. Although the ionization from Compton electrons in the magnetic conjugate region is not large, the effects on the propagation of electromagnetic waves, especially those of lower frequencies, can be important.
10.51 Many of the neutrons produced in a nuclear explosion above 15 miles will travel upward, escaping to high altitudes. Since neutrons are not affected by the geomagnetic field, they spread over a large region. A free neutron disintegrates spontaneously, with a half-life of about 12 minutes, into a proton and an electron (beta particle). The latter will be trapped by the geomagnetic field lines and will produce ionization in the D-region after following a field line into the atmosphere, either in the vicinity of the explosion or at the magnetic conjugate. The ionization levels produced by neutrons in this manner are low, but they have been detected at distances of several thousand miles from the burst point. From the times at which the effects were observed, they could have been caused only by neutrons.
10.52 Thermal X rays begin to escape from the fireball for detonations in the upper portion of the 10 to 40 miles altitude regime and can cause appreciable ionization in the E-region above the burst point. Ionization in the E- and F-regions will be perturbed by traveling disturbances to a greater extent from detonations in this altitude regime than from explosions of similar yield below 10 miles. A high-yield detonation near 40 miles altitude may produce a region of severe electron density depletion (§ 10.71 et seq.). Fireballs rising above 65 miles and beta particles escaping from fission debris above 40 miles also increase the electron density in the E and F-regions.
DETONATIONS AT 40 TO 65 MILES ALTITUDE
10.53 X rays ionize a region of considerable extent around a detonation in the 40 to 65 miles regime. The mechanism of fireball formation changes appreciably in this range (§ 2.130 et seq.), since at 65 miles the X-ray stopping altitude has been exceeded, and the radiation can spread very widely. Starting at about 50 miles altitude, the interaction of the expanding weapon debris with the atmosphere becomes the dominant mechanism producing a fireball. Above about 50 miles, the geomagnetic field will influence the location and distribution of the late time fireball, as will be seen shortly. The 40 to 65 miles altitude regime is also a transitional one for deionization mechanisms in the fireball, and for the dynamic motion of the rising fireball.
10.54 Above about 40 miles, the temperature of the fireball is no longer the governing factor in ionization. The electron density changes only in accordance with the increase in volume of the fireball, thus causing a wider distribution of the free electrons in space. Recombination of electrons with positive atomic ions, produced by the high temperatures in the fireball, is the main removal process. This is, however, much slower than the recombination with molecular ions which predominates in the normal D- and E-regions. Electron densities greater than 108 electrons/cm3 can then persist for tens of seconds, resulting in significant attenuation and refraction of electromagnetic waves. The persistence depends on how rapidly the fireball volume increases and on the detailed chemistry of the fireball gasses.
10.55 For explosions of high and moderately high yields at altitudes near the upper limit of the regime under consideration, the fireball may rise to heights of hundreds of miles (see Figs. 10.158b and c). At these heights, the fireball and debris regions will be affected by the geomagnetic field lines (§ 10.63 et seq.). For smaller yields, the fireball generally rises buoyantly and smoothly to a nominal stabilization altitude, with no overshoot (Fig. 10.158a). A spreading velocity of 165 feet per second is frequently used to make rough estimates of debris motion for stabilization altitudes between 50 and 125 miles. If more than a rough estimate is required, upper-altitude wind information must be used to calculate the spreading velocity.
10.56 The region identified for lower altitude bursts as that around the fireball now merges into the D-, and E-, and F-regions. Hence, it will not be discussed separately here or in the next section which is concerned with nations above 65 miles altitude.
10.57 The D-region is more widely influenced by prompt radiation from detonations above 40 miles than from detonations below that altitude, since both X-rays and neutrons have longer penetration distances at the higher altitudes. For detonations above 40 miles, X rays produce essentially all the prompt ionization in the D-region. As indicated in § 10.43, fast neutrons are apparently the main source of prompt ionization in this region for detonations at somewhat lower altitudes.
10.58 Continuing ionization of the D-region by delayed gamma rays and beta particles is of major importance when the burst altitude is between 40 and 65 miles. The situation is similar to that described in § 10.47 for the case in which the debris rises to a height of more than 40 miles. The beta-particle ionization is restricted to areas in the D-regions of both hemispheres of the earth, which are each roughly equal to the area of the debris. The delayed gamma rays spread in all directions, however, and the ionization in the D region near the burst point is consequently more extensive in area but is less intense than that due to the beta particles. The upward motion of the debris can allow the gamma rays to irradiate areas of the D-region several hundred miles in radius. It is apparent that the electron densities resulting from such widespread irradiation will generally be low.
10.59 Compton electrons from delayed gamma rays and beta particles formed by the spontaneous disintegration of neutrons can cause widespread, although relatively weak, ionization in the D-region near the burst point and also at its magnetic conjugate. The general effects are similar to those described in §§ 10.50 and 10.51 for nuclear detonations at lower altitude.
10.60 Detonations above 40 miles, and particularly those above 50 or 55 miles, will irradiate the E-region extensively with X rays. Consequently, there will be prompt ionization, with the usual fairly long E-region recovery time, in addition to that caused by the continuing radiation from the radioactive debris. Ionization effects in the E region, similar to sporadic-E (§ 10.12), have been noted following detonations above 40 miles.
10.61 Strong F-region disturbances, involving an initial increase followed by a decrease in electron density, were observed over an area of more than a thousand miles in radius for many hours after the TEAK megaton-range burst at about 48 miles altitude(§ 2.52). The proposed explanation for these disturbances is given in § 10.71 et seq. There also appeared to be an effect similar to spread-F (§ 10.12) which ended at sunrise, and some tilting of the normal ionospheric stratification which altered the path of reflected radio signals. Similar but less severe effects were noted after subsequent high-altitude explosions.
DETONATIONS ABOVE 65 MILES
10.62 The mechanisms of fireball formation and growth continue to change as the detonation altitude increases above 65 miles. At these altitudes, X rays travel great distances in the very low-density atmosphere and do not produce a normal fireball. Below about 190 miles, depending on the weapon yield, the energy initially appearing as the high outward velocity of debris particles will still be deposited within a fairly short distance. This results in the formation of a heated and ionized region. The apparent size of this so-called “fireball” region may depend on the manner in which it is viewed. The optical (or radiating) fireball may not coincide with the radar fireball, i.e., the region affecting radar signals, and. the fireball boundary may not be well defined. Because of the large dimensions, times of the order of a few seconds may be required before the initial motion of the debris is reduced significantly.
10.63 The geomagnetic field plays an increasingly important role in controlling debris motion as the detonation altitude increases. Above about 300 miles, where the density of the atmosphere is very low, the geomagnetic field is the dominant factor slowing the outward expansion of the weapon debris. This debris is initially highly ionized and is consequently a good electrical conductor. As it expands, it pushes the geomagnetic field out ahead of it, and the magnetic pressure caused by the deformation of the field can slow down and stop the debris expansion. The debris may expand hundreds of miles radially before being stopped by the magnetic pressure. The problem of the expansion of ionized debris against a magnetic field is quite complex. Instabilities in the interface between the expanding debris and the geomagnetic field can cause jetting of debris across field lines, and some debris can escape to great distances.
10.64 Debris initially directed downward will be stopped by the denser air below the burst point at an altitude of about 70 miles, whereas upward-directed debris travels for long distances. If, in being stopped by the atmosphere, the downward-directed debris heats and ionizes the air, that heated region will subsequently rise and expand. Some upward-directed, ionized debris will follow geomagnetic field lines and will reach the conjugate region in the other hemisphere of the earth.
10.65 The geomagnetic field will also play an important role in determining the continued growth and location of the ionized region once it has formed. Expansion along the field lines can continue after expansion across the field has stopped. Arcs (or tubes) of charged particles, mainly beta particles, may be formed, extending from one hemisphere to the other. Ionization will then occur in the upper atmosphere in each conjugate region. This may happen even for detonations below 65 miles if the fire ball is still highly ionized after it reaches altitudes of a few hundred miles.
10.66 Within the fireball, the rapidly moving debris ions cause ionization of the air; each such ion can ionize many air molecules and atoms before losing its kinetic energy. Because of the reduced air density above 65 miles, the initial ionization within the fireball is less than for detonations at lower altitudes. However, if expansion is largely along the geomagnetic field lines, decrease in electron density due to volume expansion may be relatively slow. Dimensions across the geomagnetic field are typically a few hundred miles after a few minutes.
10.67 As stated in § 10.54, electron recombination with positive atomic ions will proceed slowly, and electron densities in the fireball high enough to produce attenuation of radar signals may last up to a few minutes. Electron densities sufficient to affect electromagnetic signals of lower frequency may persist much longer. The formation, location, and extent of the ionized regions are dependent both on weapon characteristics and atmospheric composition and are difficult to predict.
10.68 Apart from the ionization within the fireball region due to the kinetic energy of the debris ions, the radioactive debris causes ionization (in the D-region), after the initial expansion has ceased. This ionization results from the emission of beta particles and delayed gamma rays. Hence, the location of the debris after the initial expansion is important.
10.69 Neutrons and X rays travel ing downward from a burst above about 65 miles altitude will irradiate large areas of the D-region. Some widespread ionization of low intensity will also be caused by the decay of neutrons in the earth's magnetic field, as described in § 10.51.
10.70 The debris that is initially directed upward or jets across the field lines will be in a position to release beta particles in locations and directions suitable for trapping in the earth's magnetic field. These particles, traveling back and forth along the field lines and drifting eastward in longitude around the earth, will spread within a few hours to form a shell of high-energy beta particles, i.e., electrons, completely around the earth (§ 2.147).
INDIRECT EFFECTS OF HIGH-ALTITUDE EXPLOSIONS
10.71 The electron density in the E and F-regions of the ionosphere may be changed by effects associated with a nuclear explosion other than direct ionization. The most important of these effects are hydrodynamic (shock) and hydromagnetic disturbances (see § 10.26 footnote) and changes in air chemistry. As the shock wave from the detonation propagates through the atmosphere, the air in a given region experiences first a compression phase and then a suction phase (§ 3.04). During the compression phase, the density of the air, and hence of the electrons present, increases because of the decrease in volume. However, the combined effect of heating by compression and of expansion of the air during the suction phase may be a decrease in the electron density below the normal value.
10.72 The TEAK high-altitude shot produced a shock wave which propagated for several hundred miles from the burst point. As the shock passed a particular location, the electron densities in the E- and F-regions first increased and then decreased well below normal until local sunrise (§ 10.61). Changes in the chemistry of the atmosphere may have been partly responsible for the decrease in electron density.
10.73 As the shock wave slows down, it eventually becomes an acoustic (or sound) wave, often called a gravity acoustic wave because it is propagated in a medium (the atmosphere) whose density variation is determined by gravity. Acoustic waves travel thousands of miles from the burst point and can cause perturbations in the E- and F-regions at great distances. These perturbations are evidently hydromagnetic in nature, since the electron densities, which are difficult to calculate, are apparently dependent on the direction of propagation of the acoustic waves relative to the local geomagnetic field lines.
10.74 As well as causing ionization, X rays from a nuclear explosion, like gamma rays, can produce excited states (§ 8.23) of atoms and molecules of the air in the E- and F-regions. These excited neutral particles can undergo chemical reactions which affect electron densities. If the detonation altitude is above about 200 miles, the resulting changes can be widespread and may last for several hours. The moderate decrease in electron density in the F region, observed out to more than 600 miles from the burst point after the STARFISH PRIME event (1.4 megatons at 250 miles altitude), has been attributed to changes in air chemistry caused by X rays.
EFFECTS ON RADIO AND RADAR SIGNALS
SIGNAL DEGRADATION
10.75 Nuclear explosions can degrade, i.e., attenuate, distort, or interfere with, signals from radar, communication, navigation, and other systems employing electromagnetic waves propagated through the atmosphere. In general, systems that depend on the normal ionosphere for propagation by reflection or scattering, as will be described in due course, can be affected over large areas for periods ranging from minutes to hours following a single burst at high altitude. Electromagnetic waves that pass through the ionosphere, but do not rely on it for propagation, e.g., satellite communication and some radar systems, can also be affected, but usually only over localized regions and for periods of seconds to minutes. Systems which use waves that propagate below the ionosphere, along lines-of-sight between ground stations or between ground stations and aircraft, will not, in general, experience signal degradation.
10.76 The signal strength required for acceptable systems performance is usually given in terms of a signal-to noise ratio. The term “noise” refers to random signals that may originate within the receiver itself or may arise from external sources, usually thunder storms and other electrical disturbances in the atmosphere. Nuclear explosions can also generate noise. When the signal-to-noise ratio falls below a minimum acceptable level, system degradation occurs in the form of increased error rate, e.g., symbol or word errors for communications systems and false or missed targets for radars. As the result of a nuclear explosion, the signal-to-noise ratio may be decreased by attenuation of the signal strength or by increase in noise (or by both).
10.77 Detailed analysis of system performance requires consideration of many factors. These include the following: the geographic and geomagnetic locations of the burst point and of the propagation paths; time variations of the electromagnetic transmission properties along these paths, i.e., propagation channel characteristics; the effect of these characteristics on the desired signal, on noise generated within the receiver, and on undesired signals reaching the receiver; the signal processing used; the system mission; and criteria of system performance.
SIGNAL ATTENUATION
10.78 Absorption of energy from the electromagnetic waves is the major source of signal attenuation following the detonation of a nuclear weapon. In general, the absorption produced by a certain electron density is related inversely to the square of the wave frequency (§ 10.130); hence, absorption is more important for low- than for high frequency systems that use the ionosphere for long-range transmission. The extent of absorption depends strongly on the location of the transmission path relative to the burst point and to the time after the burst. Shortly after the explosion, absorption may be so intense that there is a blackout and communication is impossible. This will be followed by a period of reduced system performance before fairly normal conditions are restored. The duration of the blackout, particularly for systems operating below about 30 megahertz, is generally long in comparison with that of reduced performance. Absorption may also affect received noise levels if the noise reaches the receiver via the ionosphere.
10.79 When the electron densities are decreased by the effects of a nuclear explosion, signal attenuation, especially in the frequency range between 3 and 30 megahertz, can result from loss of reflection (due to refraction) from the E and F-region. Signals which would normally reach the receiver by reflection from the ionosphere may then be only weakly refracted so that they continue into space.
NOISE
10.80 Two noise sources from a nuclear detonation are thermal radiation from the fireball and synchrotron radiation from beta particles traveling along the geomagnetic field lines. The fireball may remain at temperatures above 1,000° Kelvin for a few hundred seconds and may produce considerable noise if the antenna is pointed at the fireball. Thermal noise generally will be significant only for systems with low (internal) receiver noise. The actual noise received will depend on the properties of the fireball, e.g., whether or not it is absorbing at the frequency of interest, the amount of attenuation outside the fireball, and the directivity of the receiving antenna.
10.81 Beta particles spiraling along the geomagnetic field lines radiate electromagnetic energy in the form of what is known as “synchrotron radiation.” This covers a range of frequencies, but is much more intense at low than at high frequencies. Synchrotron radiation picked up by an antenna will produce noise in the receiver. However, the noise level is relatively weak and is not significant except for very sensitive, low-frequency systems with the antenna beam at right angles to the geomagnetic field lines.
PHASE EFFECTS
10.82 In free space, the phase velocity of an electromagnetic wave, i.e., the rate of propagation of a plane of constant phase, is equal to the velocity of light in a vacuum. In an ionized medium, however, the phase velocity exceeds the velocity of light by an amount which depends on the frequency of the wave and the electron density of the medium. If an electromagnetic signal traverses a region that has become ionized by a nuclear detonation, it will consequently suffer phase changes. A communication system that uses phase information will thus be affected. Furthermore, because the phase velocity varies with the wave frequency, a signal consisting of waves of several frequencies, as is commonly the case, will be distorted because the phase relationships between the waves will be changed.
10.83 If the propagation path passes through regions of varying electron densities, that is to say, if the electron densities encountered by the signal vary with time, a frequency shift (Doppler shift) occurs. For wide-band communications systems there may then be interference between adjacent channels. As a result, the effective (or useful) bandwidth would be decreased.
10.84 Although the phase velocity of electromagnetic waves is greater in an ionized medium than in free space, the group velocity, i.e., the velocity with which the signal energy is transmitted, is less than the velocity of light. The group velocity is also dependent on the wave frequency and the electron density of the medium. A signal passing through an ionized region thus suffers frequency-dependent time delays as compared with propagation through free space. This will cause various errors in radar systems, as will be seen in § 10.119.
REFRACTION AND SCATTERING EFFECTS
10.85 The phase change of an electromagnetic wave in an ionized medium is related to the refractive index of the wave in this medium (§ 10.125). The index of refraction in free space is unity, but in an ionized region it is less than unity by an amount that increases with the electron density, for waves of a given frequency. As a result, the direction of propagation of an electromagnetic wave is changed in passing from free space, i.e., the nonionized (or very weakly ionized) atmosphere, into a region of significant ionization. This is the basis of the refraction (or bending) of electromagnetic waves by an ionized medium described in § 10.08. The wave is always bent away from the region of lower refractive index (higher electron density) toward that of higher refractive index (lower electron density).
10.86 If an electromagnetic wave is propagated through a region of increasing electron density, i.e., of decreasing refractive index, the continued refraction may cause the wave to return to the region of low electron density from which it originally came. The wave is then said to be reflected. By increasing the electron density in the ionosphere, a nuclear detonation will change the reflection altitude of electromagnetic waves coming from the earth. Thus, systems that rely on reflection from the ionosphere for long-range communications can be adversely affected by the detonation. Even if reflected signals are not normally used, unwanted reflected signals may cause interference with the desired direct signals.
10.87 When an electromagnetic wave encounters patches (or blobs) of irregular ionization, successive reflections may lead to more-or-less random changes in the direction of propagation. This is referred to as “scattering.” The term “forward scattering” is used when the propagation after scattering is in the same general direction as before scattering. If the electromagnetic wave is scattered toward the location from which it came, the effect is described as “backscattering.”
10.88 Reflection and scattering of electromagnetic waves from ionized regions produced by a nuclear explosion can result in abnormal propagation paths between transmitter and receiver of a radio system. Multipath interference, which occurs when a desired signal reaches the receiver after traversing two or more separate paths, produces fading and signal distortion. Interfering signals, due to anomalous propagation from other radio transmitters, can increase noise levels to such an extent that the desired signal might be masked. In radar systems, changes in the propagation direction due to refraction can cause angular errors. Moreover, if a radar signal is scattered back to the receiver, it can mask desired target returns or, depending on the characteristics of the scattering medium, it may generate a false target (§ 10.120 et seq.).
RADIO COMMUNICATIONS SYSTEMS
10.89 The general category of radio systems of interest includes those in which electromagnetic waves are reflected or scattered from the troposphere (§ 9.126) or the ionosphere. Such systems are used primarily for long-distance communications; however, other uses, e.g., over-the-horizon radars, also fall in this category.
10.90 Detailed analysis of communications systems, even for the normal atmosphere, is difficult and depends largely on the use of empirical data. Measurements made during nuclear tests have shown that both degradation and enhancement of signals can occur. The limited information available, however, has been obtained in tests for weapon yields and detonation altitudes which were not necessarily those that would maximize the effects on communications systems.
10.91 It is convenient to discuss radio system effects in accordance with the conventional division of the radio frequency spectrum into decades of frequency ranges. These ranges, with associated frequencies and wavelengths, are given in Table 10.91. Radar systems, which normally employ the frequency range of VHF or higher, are treated separately in § 10.114 et seq.
| Name of Range | Frequency Range* | Wavelength Range | |
|---|---|---|---|
| Very Low Frequency | VLF | 3-30 kHz | 107-106 cm |
| Low Frequency | LF | 30-300 kHz | 106-105 cm |
| Medium Frequency | MF | 300-3,000 kHz | 105-104 cm |
| High Frequency | HF | 3-30 MHz | 104-103 cm |
| Very High Frequency | VHF | 30-300 MHz | 103-102 cm |
| Ultra High Frequency | UHF | 300-3,000 >MHz | 102-10 cm |
| Super High Frequency | SHF | 3-30 GHz | 10 - 1 cm |
| Extremely High Frequency | EHF | 30-300 GHz | 10 - 1 mm |
*The abbreviations kHz, MHz, and GHz refer to kilohertz (104 cycles/sec), megahertz (106 cycles/ sec), and gigahertz (109 cycles/sec), respectively.
VERY-LOW-FREQUENCY RANGE (3 to 30 kHz)
10.92 The frequencies in the VLF band are low enough for fewer than 100 free electrons/cm3 to cause reflection of the signal (§ 10.20). The bottom of the ionosphere thus effectively acts as a sharp boundary which is not penetrated, and the electromagnetic radiation is confined between the earth and the ionosphere by repeated reflections. The resulting “sky wave,” as it is called, may be regarded as traveling along a duct (or guide) whose boundaries are the earth and that level in the atmosphere at which the electron density is about I00 electrons per cubic centimeter. There is also a “ground wave” whereby the signal is transmitted along the surface of the earth and tends to follow its curvature. Global VLF broadcast communications and maritime and aerial navigation systems use the long propagation distances that are possible because ground wave attenuation is relatively low and the sky wave is reflected at the bottom of the ionosphere with little absorption.
10.93 The major effect of nuclear detonations is to cause ionization i.e., an increase in electron density, which may lower the ionospheric reflection altitude. Theoretical analyses and experimental data indicate that the major consequences are phase anomalies and changes in signal strength and in the noise from distant thunderstorms. These effects are expected to persist longer in the daytime than at night because of the slower decay of the electron density, assuming the same weapon yield and burst altitude.
10.94 Phase changes may be large and rapid, e.g., 1,000 degrees or so within a millisecond, and they are followed by a slow recovery of a few degrees per second. Such phase changes may be significant for navigation, synchronous communications, and phase modulation systems. VLF systems operating over short, medium, or long distances can be affected by the phase changes that result from the ionization produced by a nuclear explosion.
10.95 On paths of medium length, where both ground and sky waves are received, the change in phase of the sky wave may result in mutual interference of the two signals. There will then be a reduction in the strength of the processed signal. Over relatively short transmission paths, when only the ground wave is normally used, the change in reflection altitude may cause the sky wave to be received. This may enhance or interfere with the ground wave, according to circumstances. For long-distance VLF communications, when only the sky wave is important, a nuclear explosion can cause large phase changes even at a distance. Thus, after the TEAK and ORANGE high-altitude shots (§ 2.52), the 18.6-kilohertz signal transmitted from the Naval Radio Station at Seattle, Washington, to Cambridge, Massachusetts, suffered an abrupt phase shift. The entire path was at least 3,000 miles from the burst points.
10.96 Distant thunderstorms produce some atmospheric noise in the VLF band, the noise level depending on the ionospheric reflection height. Hence, a change in this height can affect the signal-to-noise ratio. The system degradation or improvement following a nuclear detonation will depend on the relative geographic locations of the signal source, the noise source, the ionization produced, and the propagation path. Reduction of the signal-to-noise ratio appears to be significant primarily for long transmission paths with ionospheric reflection. A single high-altitude explosion or multiple explosions which produce ionization affecting appreciable portions of a propagation path will result in maximum degradation.
LOW-FREQUENCY RANGE (30 TO 300 kHz)
10.97 As the electromagnetic wave frequency is increased above 30 kilohertz, the normal ionosphere behaves much less as a sharp boundary. The wave penetrates several miles before being reflected back toward the earth. The altitude to which the wave penetrates and the attenuation normally experienced depend strongly on the magnitude and the rate of vertical change, i.e., the gradient, of electron density at the bottom of the ionosphere. Reflection extends the useful range of propagation, particularly at night when ionization in the lower D-region is normally absent. Attenuation of the sky wave increases in the daytime, especially for the higher frequencies because of their greater penetration. Although ground waves are commonly used for LF transmissions, sky waves often provide acceptable signals a few thousand miles from the transmitting station.
10.98 Ionization from nuclear explosions will generally not degrade the performance of LF systems which normally depend only on the ground wave unless the change in reflection altitude causes the sky wave to be received. As with VLF, this may enhance or interfere with the ground wave according to the circumstances; however, reception of the sky wave is less likely for LF than for VLF. Systems which rely on sky wave propagation may experience attenuation lasting from a few minutes to several hours. For a given yield and burst height, the duration of the disturbance may be expected to be greatest in the daytime. The most severe attenuation appears to occur for long paths, when ionization produced by the detonation effects appreciable portions of the propagation path. Furthermore, large phase shifts can occur.
MEDIUM-FREQUENCY RANGE (300kHz TO 3 MHz)
10.99 Normal propagation in the MF band is characterized by large attenuation of sky waves in the daytime, limiting communication at such times to ground waves. Increase of ionization in the D-region from high-altitude nuclear explosions will cause further attenuation of MF sky waves, and propagation may be limited to the ground wave during both day and night. In regions near the burst (or its magnetic conjugate) the sky wave may be blacked out for hours. Since atmospheric noise propagated by the ionosphere is a principal source of interference, absorption in the D-region may improve ground-wave reception for some paths. However, the limiting signal-to-noise ratio is determined primarily by local thunderstorm activity. Reduction of noise from distant thunderstorms will thus not improve marginal reception.
HIGH-FREQUENCY RANGE (3 TO 30 MHz)
10.100 The HF band is used extensively for long-range communications; the frequencies are high enough to permit transmission of information at a rapid rate and yet are sufficiently low to be reflected by the ionosphere. The signals are propagated from the transmitter to a receiver by successive reflections from the E- or F-region and the surface of the earth. Electromagnetic waves with frequencies toward the lower end of the HF range are normally reflected from the E-region of the ionosphere after suffering some attenuation by absorption in the D-region. Reflection at the upper end of the range requires higher electron densities and occurs from the F-region (§ 10.135).
10.101 If a nuclear explosion increases the electron density in the D region above its usual maximum value of about 103 electrons/cm3, signal attenuation by absorption will be increased. Furthermore, the increase in electron density may lower the reflection altitude and thus change the propagation path of the signal. Communications (and other) systems using the HF range can thus be seriously degraded. Disturbances resulting from an increase in the D-region electron density will persist longer in the daytime than at night, but decreases in the E- and F-regions may reverse the situation (§ 10.105).
10.102 Both prompt and delayed radiation from a nuclear burst can produce sufficient ionization to cause blackout of HF signals, lasting from a few seconds to several hours. The recovery time depends, among other things, on the weapon yield and the detonation altitude. The period during which the system is degraded is greater for lower than for higher frequencies, because a higher electron density is required in the latter case, and it increases with the number of times the propagation path traverses the region of enhanced ionization.
10.103 The effect of prompt radiation is greatest for high-altitude explosions. Thus, a megaton burst at a height of 200 miles in the daytime would be expected to disrupt HF systems out to a distance of about 1,500 miles from the burst point. Recovery would require from a few hundred to a few thousand seconds, depending on the explosion yield, the signal frequency, and the number of traversals of the D-region made by the electromagnetic wave in its successive reflections from transmitter to receiver.
10.104 The signal degradation due to delayed radiations also varies with the explosion yield and altitude. For weapons detonated at low altitudes, in which the radioactive residues do not rise above 15 miles, the effects on HF systems will generally be small, except for propagation paths close to the burst point. If the debris reaches an altitude above 15 miles but below about 35 to 40 miles, the D-region above the debris will be ionized by delayed gamma rays and possibly by beta particles(§ 10.46). Should the debris rise above 40 miles, the beta particles will cause ionization both in the burst region and in the magnetic conjugate region. In the low-altitude detonation of weapons of large yield, the debris may rise above 15 miles and significant attenuation of HF signals can occur for propagation paths within several hundred miles of the burst point. For high-altitude detonation of such weapons, blackouts may persist for many hours over regions thousands of miles in diameter. Even kiloton-yield detonations at very high altitudes may cause daytime blackout of HF systems over considerable areas for periods of minutes to tens of minutes.
10.105 Nuclear explosions may also affect HF communications by a decrease in the electron density in the E and F-regions which changes their reflection characteristics. Following the TEAK shot (in the D-region), the maximum usable frequency for long-distance communication was reduced over an area some thousands of miles in radius for a period lasting from shortly after midnight until sunrise (cf. § 10.72). Such severe changes in the reflection properties of the ionosphere were not noted, however, during the FISHBOWL high-altitude test series (§ 2.52). Nevertheless, electron depletion in the E- and F-regions is expected to be a significant degradation factor following large-yield detonations above about 65 miles during the nighttime. Restoration of the normal electron density following a daytime explosion of the same type should occur more rapidly.
10.106 For three events at the highest altitudes in the FISHBOWL series, a number of new propagation modes were noted; in some cases the use of exceptionally high frequencies, well into the VHF range, became possible. When such modes were in existence, in addition to the normal modes, considerable multipath propagation was experienced. The usefulness of the new modes depends markedly on the relative geometry of the transmitter and receiver, and on the reflection mechanism.
10.107 It is important to mention that, although HF communications can be degraded seriously by a nuclear explosion at high altitude, radio systems operating in this band may still be able to perform substantial portions of their mission in some circumstances. It is by no means certain, for example, that HF systems will be blacked out completely if the transmission path is at some distance from the burst point.
VERY-HIGH-FREQUENCY RANGE (30 TO 300 MHz)
10.108 Signals in the VHF range penetrate the normal ionosphere and escape from the earth. Consequently, this frequency range is primarily used for line-of-sight communications over short distances, e.g., commercial television channels and FM radio, but long-range communication is possible by making use of the small amount of transmitted energy that is scattered back to earth in a forward direction by patches of unusually intense ionization. Forward propagation ionospheric scatter (FPIS) systems are inefficient, since only a minute fraction of the energy of the transmitter reaches the receiver, but they make additional portions of the electromagnetic spectrum available for fairly reliable communication between ground stations at distances up to 1,500 miles apart.
10.109 Normally, VHF signals scatter from ionization irregularities caused by meteor trails or by turbulence in the upper part of the D-region. Since scattering from meteor trails occurs at altitudes of about 60 miles or more, the propagation path must traverse the region of maximum absorption (around 40 miles altitude) caused by delayed gamma and beta radiation from a nuclear burst. Meteor-scatter circuits normally operate with fairly small signal margins, and so absorption effects can be important.
10.110 Signals in FPIS systems scattered from irregularities in electron density caused by turbulence may be enhanced by the increased ionization from a nuclear explosion. However, absorption will reduce the signal return from normal scatter heights to negligible magnitudes for only a short period of time. New propagation modes, produced by reflection from increased ionization in the F-region or by fireball ionization, can cause a multipath condition which will reduce the effective circuit bandwidth. Following the KING FISH event (submegaton yield in the E-region), the Midway-to-Kauai ionospheric-scatter circuit in the Pacific was required to operate on a reduced band width for 21 minutes. Pacific FPIS systems also experienced about 30 seconds of blackout following the STARFISH PRIME test (§ 10.74).
10.111 Line-of-sight propagation traversing the D-region, e.g., satellite communications, can be degraded by absorption due to an increase in electron density arising from delayed radiation. The degradation may last for tens of minutes over regions of hundreds of miles in radius. Attenuation and signal distortion caused by fireball regions above about 60 miles may also affect communication systems operating in the VHF band.
ULTRA-HIGH FREQUENCY RANGE (300 MHz TO 3 GHz)
10.112 In the UHF band (and the upper part of the VHF band), forward scattering by neutral molecules and small particles in the troposphere (below about 12 miles) is used to extend propagation beyond the line of sight. Weapons detonated above the troposphere are not expected to affect tropospheric propagation paths. Bursts at lower altitude may cause degradation for a few seconds if the fireball rises through the propagation path. Significant multipath propagation due to increased ionospheric ionization appears unlikely.
10.113 Line-of-sight propagation through the ionosphere, such as is used by UHF satellite links, can be degraded if the propagation path passes through or near the fireball. Ionization by delayed radiation, especially beta particles, can produce absorption lasting a few minutes over regions of from tens of miles to a few hundred miles in radius. If the ground-to-satellite propagation path moves rapidly, the degradation period will depend primarily on the relative geometry of the path and the disturbed region. Wide-band satellite signals can be degraded by signal distortion.
RADAR SYSTEM EFFECTS (VHF AND ABOVE)
10.114 Radar systems are similar to radio communications systems in the respect that a transmitter and receiver of electromagnetic waves are used. However, in radar the receiver is located near the transmitter and may use the same antenna, which typically is highly directional. The transmitted signal, consisting of a series of pulses, is in part reflected back to the receiver, like an echo, by objects in the path of the pulsed beam. From the direction of the antenna, the travel time of the signal, and its speed of propagation, information can be obtained concerning the location and movement of the source of the echo. Frequencies normally employed in this connection are in the VHF range and above. There is little effect of ionization on signals of these frequencies provided both the radar and the target are below the ionosphere.
10.115 If the signal must pass through the ionosphere, however, the interference from nuclear detonations becomes important. Radar signals traversing the ionosphere will, like radio signals, be subject to attenuation. Although any additional attenuation is undesirable, the amount which can be tolerated varies widely with the type of radar and the purpose of the system. In search radars, for example, where it is desired to detect each target at the greatest possible range, i.e., just as soon as the target return becomes observable against the background noise, even the smallest additional signal loss results directly in shortening of the range at which a given target can be detected. A tracking or guidance radar in a weapon system, on the other hand, usually takes over its target, well inside its maximum detection range, from another (search) radar which has already detected and tracked the object. In this case the signal can be attenuated to a much greater degree before the radar loses its ability to acquire or track.
10.116 A large amount of attenuation by absorption occurs when the propagation path traverses a fireball. The attenuation is determined by the properties of the fireball and these are strongly dependent on altitude. In general, it can be said that fireballs will be opaque to radar signals operating at frequencies of 10 gigahertz ( 104 megahertz) and below, for periods of tens of seconds to a few minutes.
10.117 The ionized atmosphere surrounding the fireball will absorb radar frequencies below a few gigahertz, i.e., a few thousand megahertz, when the fireball is above about 10 miles. A smaller region adjacent to the fireball will have the same effect for detonations at lower altitudes (§ 10.36). The degree and areal extent of the absorption can be calculated with reasonable reliability but lengthy computations are required.
10.118 Although absorption is generally the main source of degradation of radar systems, there are a number of other mechanisms which may be important in some cases. For example, the signal path may be bent by refraction when the electromagnetic wave traverses a medium in which the electron density changes along the path length. As a result, directional errors can occur. This effect may be significant if the signal passes close to the fireball, but outside the region in which absorption predominates, where the electron gradients are large, or if the signal traverses the E-region where the electron density is high and the rate of collision with other particles is low (§ 10.137).
10.119 The velocity of propagation of the radar signal that is detected is equal to the group velocity of the electromagnetic wave described in § 10.84; this determines the travel time of the signal from the transmitter to the target and back. Changes in the group velocity as a result of propagation through an ionized medium will change the signal travel time and will introduce an error in estimating the range of the target. Since the change in the group velocity varies with the wave frequency, radar systems using wide bandwidths will have different travel times over the range of frequencies present in the signal. The return signals will then arrive at different times, leading to what is called “dispersion.” The phenomenon is characteristic of transmission through a highly ionized medium and causes substantial range errors.
10.120 The fireball and the charged particles in the tube enclosed by the geomagnetic field lines (§ 10.65) may reflect or scatter radar waves, thus producing spurious signals which may be confused with target return signals. This effect, known as “clutter,” may occur by reflection from rapidly changing gradients of electron density or as backscatter from irregular patches of ionization or from particulate matter thrown into the air when a fireball touches the surface. Clutter returns may be so intense as to affect radars in the same way that terrain features sometimes cause difficulties by reflecting energy back to the receiver thereby masking weak targets.
10.121 If part of the energy of the radar pulses returning from a target experiences forward scattering through small angles, the signals reaching the receiver will fluctuate both in phase and amplitude. The resulting effect is referred to as “scintillation.” The phase fluctuations are equivalent to fluctuations in the angle of arrival of the signals, so that the apparent position of the target will appear to move somewhat randomly. The amplitude fluctuations make target identification difficult for the signal processing system.
SUMMARY OF NUCLEAR DETONATION EFFECTS
10.122 The general effects of nuclear detonations on the various radio frequency ranges used in radio and radar systems are summarized in Table 10.122.
| Frequency Bane | Degradation Mechanism | Spatial Extent and Duration of Effects* | Comment |
|---|---|---|---|
| VLF | Phase changes, amplitude changes | Hundreds to thousands of miles; minutes to hours | Ground wave not affected, lowering of sky wave reflection height causes rapid phase change with slow recovery. Significant amplitude degradation of sky wave modes possible. |
| LF | Absorption of sky waves, defocusing | Hundreds to thousands of miles; minutes to hours | Ground wave not affected, effects sensitive to relative geometry of burst and propagation path |
| MF | Absorption of sky waves, defocusing | Hundreds to thousands of miles; minutes to hours | Ground wave not affected |
| HF | Absorption of sky waves, loss of support for F-region reflection, multipath interference | Hundreds to thousands of miles, burst region and conjugate; minutes to hours | Daytime absorption larger than nighttime, F-region disturbances may result in new modes, multipath interference |
| VHF | Absorption, multipath interference, or false targets resulting from resolved multipath radar signals | Few miles to hundreds of miles; minutes to tens of minutes | Fireball and D-region absorption, FPIS circuits may experience attenuation or multipath interference |
| UHF | Absorption | Few miles to tens of miles; seconds to few minutes | Only important for line-of-sight propagation through highly ionized regions |
*The magnitudes of spatial extent and duration are sensitive functions of detonation altitude and weapon yield.
TECHNICAL ASPECTS OF RADIO AND RADAR EFFECTS 3
DENSITY OF THE ATMOSPHERE AND ALTITUDE
10.123 The decrease in density of the atmosphere with increasing altitude can be represented approximately by the equation
where $\rho(h)$ and $\rho_0$ are the densities, in g/cm3 at height $h$ and at sea level, respectively, and $H_\rho$ is called the scale height; $h$ and $H_\rho$ must be expressed in the same units of length, e.g., miles. Because both temperature and composition of the air change with altitude, the scale height is not actually a constant. However, below about 60 miles, use of a constant density scale height of 4.3 miles in equation (10.123.1) gives a fairly good representation of the change in atmospheric density with altitude. For higher altitudes the density scale height increases, i.e., the density varies more slowly with altitude, but since altitudes below 60 miles are of primary interest for the present purpose, the simple exponential relationships with constant scale height will be employed.
10.124 By setting Hp in equation (10.123.1) equal to 4.3 miles, the result is
and this expression, with h in miles, will be used later. If the base of the exponent is changed from e to 10, where e = 10-2.3, then
\[ \rho (h) \;\approx\; \rho_0 l0^{-W43 \times 2.3} \;\approx\; \rho_0 10^{-W10} \]It follows, therefore, that in the altitude range of interest, the density of the atmosphere decreases approximately by a factor of 10 for every 10 miles increase in altitude. Thus, at an altitude of 40 miles the air density is about 10-4 and at 60 miles roughly 10-6 of the sea-level density.
ATTENUATION AND REFRACTION OF ELECTROMAGNETIC WAVES
10.125 The propagation of electromagnetic waves of a given frequency through a medium can be described in terms of a “complex” index of refraction, consisting of a real part and an imaginary part. The real part is a phase factor which determines the phase shift and ordinary index of refraction, i.e., the ratio of the phase velocity of the electromagnetic waves in a vacuum to that in the given medium. The imaginary part, on the other hand, is related to the attenuation of the waves by absorption in the medium. From the equations of motion of electromagnetic waves, it is possible to derive expressions for the index of refraction and for the attenuation in an ionized medium. Appropriate forms of these expressions are given and discussed below, with special reference to the effects of nuclear explosions on the ionization of the atmosphere.
10.126 Attenuation of electromagnetic (and other) signals is commonly stated in terms of decibels; thus,
\[ \text{Attenuation in decibels } = 10 \log \frac{ P_{\text{in}}}{ P_{\text{out}}}, \]where $P_{\text{in}}$ is the signal power (or strength) before attenuation and $P_{\text{out}}$ is that after attenuation. An attenuation of 10 decibels implies that the signal strength has been reduced to 10-1, 20 decibels to 10-2, 30 decibels to 10-3, and so on, of the original strength. A decrease of 20 to 40 decibels, depending on the original signal power and the noise level, will generally result in serious degradation of communications. As a rough guide, it may be taken that an attenuation of 30 decibels will reduce substantially the effectiveness of a radio or radar system.
10.127 From the theory of the propagation of electromagnetic waves through an ionized medium, it is found that the signal attenuation, a, in decibels per mile of travel path, is given by
where $N_e$ is the electron density, i.e., number of electrons per cubic centimeter, $v$ is the number of collisions per second which an electron makes with ions, molecules, or atoms, and $\omega$ is the (angular) frequency of the wave (in radians per second). It follows from equation (10.127.1) that if the collision frequency $v$ is small then, for a given wave frequency, $a$ will be small because of the $v$ in the numerator. On the other hand, if $v$ is very large, $a$ will again be small because of the $v^2$ in the denominator. Thus, the attenuation passes through a maximum for a particular value of the electron collision frequency.
10.128 Since the collision frequency is proportional to the density of the air, it will decrease exponentially with altitude. It is to be expected, therefore, that the values of v for which attenuation of signals is important would occur only within a relatively narrow altitude region. Theoretical studies show that the attenuation of radio and radar signals caused by nuclear explosions occurs mainly within a 10-mile range centered about an altitude of 40 miles. Hence, by confining attention to the situation in the neighborhood of a 40 mile altitude, it is possible to avoid complexities and yet present a reasonably accurate picture of the effects of the burst on electromagnetic signals.
10.129 There are two exceptions to the foregoing generalizations: (1) attenuation within or close to the fireball or debris regions, and (2) nighttime attenuation by ionization resulting from prompt radiation. In the former case, the altitude of the region of maximum attenuation is governed by the altitude and size of the fireball or debris region. In the second case, the altitude of peak attenuation is about 55 miles, but since the electron density due to delayed radiation is dominant at night after only a few seconds, the prompt ionization can be ignored. The present treatment will, therefore, be mainly concerned with the 10-mile range of the atmosphere centered at an altitude of 40 miles.
10.130 For electromagnetic wave frequencies greater than about 10 megahertz, v2 at an altitude of 40 miles may be neglected in comparison with w2 in the denominator of equation (10.127.1); this equation then reduces to
so that the attenuation (in decibels) is approximately proportional to the electron collision frequency. At 40 miles altitude, the latter is roughly 2 × 107 per second. Upon inserting this value for $v$ in equation (10.130.1) and converting the wave frequency from radians per second to megahertz, the result is
\[ a = 4 \times 10^{-2} \frac{N_e}{f^2} \text{ decibels per mile,} \]where $f$ is the wave frequency in megahertz, i.e., $10^{-6} \omega/2\pi$. If the signal beam has an angle of incidence $i$, referred to the vertical, and the ionized region is 10 miles thick, the total attenuation, $A$, is
for frequencies greater than about 10 megahertz.
10.131 The collision frequency used above is for electron collisions with neutral particles, since these pre-dominate at 40 miles altitude. For electron densities greater than about 109 electrons/cm3, collisions of electrons with ions can be important, particularly within a fireball at or above 60 miles altitude, where the neutral particle density is low and electron-neutral collision frequencies are small. But for attenuation of electromagnetic signals in the D-region at some distance from the fireball, equation (10.130.2) is applicable.
10.132 For operational HF circuits, the value of sec 1 is about 5 under normal conditions. It follows then from equation (10.130.2) that, for a frequency of 10 megahertz, a 10-mile thick layer with an electron density of about 1.5 × 103 electrons/cm3 at 40 miles altitude will produce 30 decibels of signal attenuation. For a frequency of 30 megahertz, the same attenuation will result from an electron density of about 1.4 × 104 electrons/cm3. These electron densities may be taken as indicative of the values required to degrade HF systems. Since radars usually operate at frequencies greater than 30 megahertz and sec i generally will be less than 5, densities exceeding 105 electrons/cm3 are necessary to cause serious attenuation when the signals pass through the D-region of the ionosphere.
10.133 Consideration will now be given to the phase aspects of the propagation of electromagnetic waves through an ionized medium. Provided the electron collision frequency, v, is small in comparison with the wave frequency, w, as has been assumed above, the ordinary (real) index of refraction, n, is given by
where $e$ is the charge (4.8 × 10-10 electrostatic unit) and $m$ is the mass (9.1 × 10-28 gram) of the electron, and $f$ is the wave frequency in megahertz. Upon inserting the numerical values for $e$ and $m$, it is found that
\[ n = \left( 1 - \frac{0.8 N_e}{10^4 f^2} \right)^{1/2} \]Since electron densities are not known very accurately, this result may be approximated to
10.134 If an electromagnetic wave crosses a plane interface where the index of refraction changes sharply from 1 to $n$, a beam will be bent by an amount given by the familiar Snell's law, i.e.,
\[ \frac{\sin i}{\sin r} = n, \]where $i$ is the angle of incidence and $r$ the angle of refraction. If the index of refraction is such that $n = \sin i$, then $\sin r = l$, i.e., $r$ = 90°, and critical reflection occurs; the refraction is so large that the signal is unable to penetrate the medium. The condition for critical reflection by an ionized medium is obtained by setting n in equation (10.133.2) equal to $\sin i$; the result obtained is
For reflection of an electromagnetic signal encountering a given ionized medium, with electron density $N_e$, the frequency must be less than that expressed by equation (10.134.1). Alternatively, for reflection of a signal of specified frequency $f$, the electron density of the ionized medium must be greater than that given by this equation.4
10.135 As in § 10.132, sec i may be taken to be about 5 for an operational HF system. Hence, for a signal of 5 megahertz, at the lower end of the band, to be reflected, the electron density must exceed 104 electrons/cm3. For a frequency of 30 megahertz, the minimum density for reflection is 3.6 × 105 electrons/cm3. These densities are normally attained in the E- and F-regions of the ionosphere, respectively. A change in the electron density arising from the effects of a nuclear explosion can alter the altitude at which an electromagnetic wave is reflected and can consequently affect communications systems, as seen earlier in this chapter.
10.136 Equation (10.134.1) is applicable only when a nonionized medium is separated from an ionized one by a sharp boundary at which the change in refractive index, from 1 to $n$, occurs over a distance small in comparison to a wavelength at the propagation frequency. This condition does not exist either in the normal ionosphere or after it has been disturbed by a nuclear detonation. The refractive index does not change sharply and there is a gradual bending of the transmitted wave. In such situations, both the electron density and its gradient determine the phase (refraction) effects.
10.137 When the quantity $N_e/f^2$ is sufficiently large, electromagnetic waves can be both attenuated and refracted by the ionized medium. The effect that predominates depends on the ratio of the electron density gradient to the electron collision frequency. If this ratio is large, then the wave will be refracted, but if it is small the main effect will be attenuation. In most circumstances associated with a nuclear explosion, attenuation around 40 miles altitude predominates. At altitudes above about 60 miles, however, where the collision frequency is small and the electron density gradient moderately large, refraction may be important. Also, near the fireball but outside the absorbing region, refraction of electromagnetic. waves up to high frequencies, such as radar signals, is possible (§ 10.37). Although the collision frequency is large, the high electron density gradient is here the dominant factor. Within the fireball itself, however, electromagnetic waves are always strongly absorbed.
ELECTRON PRODUCTION BY PROMPT RADIATIONS
10.138 Consider a nuclear explosion of $W$ kilotons yield and let $k$ be the fraction of the yield radiated at a particular energy, i.e., as monochromatic radiation. For a point source of such radiation, assuming negligible scattering and no reradiation, the energy deposited (or absorbed) per unit volume of air, $E_D$, at an “observation” point at a slant distance $D$ from the explosion is
where $\rho$ is the air density at the observation altitude, $\mu_m$, is the mass (energy) absorption coefficient in air of the given radiation,5 and $M$ is the penetration mass, i.e., the mass of air per unit area between the radiation source and the observation point. This equation may be used for all forms of prompt radiation, using the appropriate value of $k$ given in Table 10.138. The fraction of the energy radiated as prompt gamma rays is small and its contribution to the electron density is generally less than the for other radiations. If the energy deposited in the air is reradiated or if the source photons or neutrons are scattered and follow a random path before depositing all their energy, equation (10.138.1) must be modified (§ 10.142).
| Radiation | k |
|---|---|
| X rays | 0.7 |
| Gamma rays | 0.003 |
| Neutrons | 0.01 |
10.139 According to Table 1.45, 1 kiloton TNT equivalent of energy is equal to 2.6 × 1025 million electron volts. Furthermore, about 3 × 104 ions pairs, i.e., 3 × 104 electrons, are produced for each million electron volts of energy absorbed in air (about 34 electron volts are required to produce an ion pair). Consequently, about 8 × 1029 electrons are produced for each kiloton of energy deposited in the air. Hence, the number of free electrons per unit volume, $N_e$, is obtained from equation (10.138.1), with $W$ in kilotons, as
with $\rho$ in grams per cubic centimeter, $\mu_m$ in square centimeters per gram, $M$ in grams per square centimeter, and $D$ in miles.
10.140 An expression for $M$ may be obtained in the following manner. Let $H_0$ (Fig. 10.140) be the altitude of the explosion point and $H$ that of the observation point which is at a distance $D$ from the burst. Then if $D'$ represents any position between the explosion and the observation point, and $h$ is the corresponding altitude, the value of $M$ in appropriate units is given by
\[ M = \int_0^D \rho(D')dD' = \frac{D}{H - H_0} \int_{H_0}^H \rho(h)dh, \]where, in deriving the second form, the curvature of the earth has been neglected. If $\rho(h)$ is now represented by equation (10.124.1), it is found that
where $D$, $H$, and $H_0$ are in miles and $\rho_0$ in grams per cubic centimeter; the factor 6.8 × 105, which is the density scale height in centimeters (slightly less than 4.3 miles), is introduced to obtain the required units (g/cm2) for $M$.

10.141 In general, the energy radiated from a nuclear explosion as gamma rays and X rays is not monochromatic but covers a range of photon energies. Hence, integration over the energy spectrum is necessary. For the range in which most of the gamma-ray energy is radiated, the mass absorption coefficient of air, $µ_m$, can be considered to be constant. But this is not the case for X-ray photons (of lower energy) for which the mass absorption coefficient is approximately inversely proportional to the cube of the energy. Furthermore, the situation is complicated as a result of energy changes that occur when the photons are scattered. For neutrons, the highest electron densities arise from elastic scattering (§ 10.43) and the necessity for summing over multiple scattering angles makes the calculations difficult, especially in an (inhomogeneous) atmosphere of changing density.
10.142 Allowance for the effects of scattering and of the energy spectrum of the radiation can be made approximately by modifying equation (10.139.1) to take the form
where $F(M)$ is an effective mass absorption coefficient which is a function of the penetration mass, $M$. Values of $F(M)/\kappa$, where $\kappa$ is a normalization factor that permits $F(M)$ for various radiations to be plotted on a single diagram, are given in Fig. 10.142. The values of $\kappa$ used are shown in the insert.

10.143 The electron densities produced by the total prompt radiation (neutrons and X rays) are obtained by summing the contributions of the individual radiations as given by the appropriate forms of equation (10.142.1). In this manner, the curves in Fig. 10.143 for electron densities at a height of 40 miles as a function of horizontal distance6 were derived for a 1-megaton explosion at various altitudes. Since the electron density is proportional to the energy yield, $W$, of the weapon, the results for other yields can be readily obtained from Fig. 10.143. In computing $M$ for this figure, the effects of a curved earth and a variable density scale height were included. The calculations show that below about 40 miles, ionization due to neutrons predominates, but for nuclear detonations at higher altitudes the X-rays produce essentially all the additional electrons from prompt ionization in the D-region.
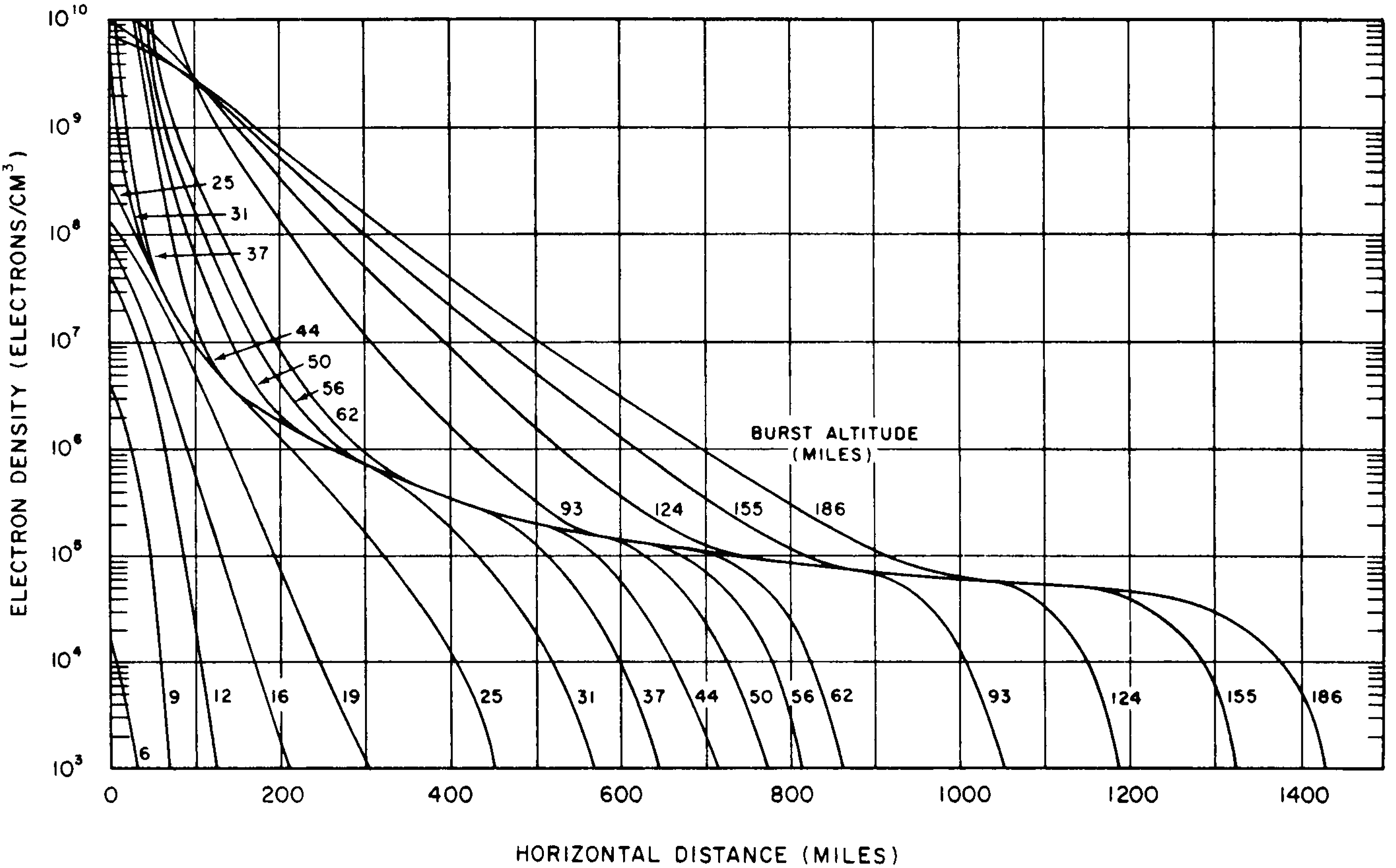
10.144 It is seen from Fig. 10.143 that at low burst altitudes, up to about 20 miles, the ionization from prompt radiation is relatively small except at short distances. At higher burst altitudes, not only does the electron density (at 40 miles altitude) for a given horizontal distance increase, but the range for a given electron density, especially above 105 electrons/cm3, increases markedly. These densities are sufficient to cause blackout of HF systems that use the sky wave for long-distance propagation. However, it will be seen (§ 10.152) that the blackout would be of relatively short duration.
RATE OF DISAPPEARANCE OF FREE ELECTRONS PRODUCED BY PROMPT RADIATION
10.145 Free electrons are removed either by attachment to neutral particles (usually molecular oxygen in the D region) or by recombination with positive ions. The electron loss by recombination is proportional to the number densities of electrons, $N_e$, and of positive ions, $N_+$, so that
where $\alpha_d$ is the recombination coefficient. Below an altitude of about 60 miles, and is approximately 2 × 10-7 cm3 sec-1.
10.146 Electron loss by attachment to molecular oxygen is proportional to the square of the atmospheric density and the number density of electrons; thus,
where $\beta$ is an attachment coefficient approximately equal to 4 × 1013 cm6g-2 sec-1. The quantity $\beta\rho^2$ is often called the attachment rate coefficient, $K$; it decreases from 6 × 107 sec-1 at sea level to about 2 × 10-3 sec-1 at 55 miles altitude.
10.147 After electrons are attached to molecules to form negative ions, they may become detached by solar radiation or by collisional processes. The rate of free electron production by detachment is proportional to the number density of negative ions, $N_-$, and the detachment source strength, i.e.,
where $S$, the detachment rate coefficient, is related to the detachment source strength. In the daytime, $S$ is approximately 0.4 sec-1 above about 35 miles altitude. Below about 35 miles the value of $S$ is uncertain but apparently it is lower by several orders of magnitude. At night, detachment is negligible at altitudes less than about 50 miles.
10.148 Negative ions formed by attachment of electrons to molecular oxygen can also react with positive ions to form neutral molecules. Since the negative and positive ion densities affect the electron density, the ion loss by recommendation must be considered. The rate of positive ion loss by recombination with negative ions is proportional to the number densities of both ions; thus,
where $\alpha_1$, usually known as the mutual neutralization coefficient, is equal to about 3 × 10-8 cm3 sec-1 above 30 miles. Below 30 miles, $\alpha_1$ is approximately proportional to the atmospheric density and is 4 × 10-6 cm3 sec-1 at sea level.
ELECTRON DENSITIES FROM PROMPT RADIATIONS
10.149 The differential equations describing the time history of electron and ion densities do not have a closed form solution. However, a number of approximations are available, and numerical solutions have been obtained with the aid of computers for particular cases. An approximate solution, which gives reasonable results for many conditions, is the so-called “equal-alpha” approximation. When ad is taken equal to a1, the electron density, $N_e(t)$, as a function of time following a pulse of prompt radiation, can be represented by
where $N_e(0)$ is the initial electron density, given by equation (10.142.1), a is an effective recombination coefficient, and t is the time after the burst.
10.150 Approximate values of $\alpha$, $S$, and $K$ in centimeter-gram-second units are given in Table 10.150 for an altitude of 40 miles in the daytime and 55 miles at night. These are the altitudes, for day and night, respectively, at which maximum attenuation of electromagnetic signals is to be expected (§ 10.129). Upon inserting the appropriate values into equation (10.149.1), the time history of electron density at the altitude of maximum attenuation is found to be
for times more than a few seconds after the burst in the daytime, and
for nighttime conditions.
| Coefficient | 40 Miles (daytime) | 55 Miles (nighttime) |
|---|---|---|
| α | 10-7 | 2 × 10-7 |
| S | 0.4 | 2 × 10-2 |
| K | 0.8 | 2 × 10-3 |
10.151 Calculations of the decay of electron densities from ionization produced by prompt radiations from a nuclear detonation have been made with a computer using numerical solutions that do not involve the equal-alpha approximation. The results for daytime conditions at a height of 40 miles are shown in Fig. 10.151; they are reasonably consistent with equation (10.150.1) provided the electron density is appreciably larger than the normal value in the ionosphere. Natural ionization sources must be considered when the electron density resulting from prompt radiation has decayed to values comparable to those normally existing at an altitude of 40 miles.
10.152 There are two aspects of Fig. 10.151 that are of special interest. First, it is seen that when the initial electron density, $N_e(0)$, is greater than 107 electrons/cm3 the electron density, $N_e(t)$, at any time more than about 1 second after the burst (in daytime) is independent of the initial value. This condition is referred to as a “saturated atmosphere.” It is to be expected from equation (10.150.1), since when $N_e(0)$ is more than 107 and t is at least a few seconds, the quantity $10^{-7} N_e(0)t$ in the denominator of the equation is greater than unity. Hence, the latter can be neglected and equation (10.150.1) reduces to
\[ N_e(t) \approx \frac{1}{3 \times 10^{-7}t} cm^{-3}, \]so that the electron density at time $t$ is independent of the initial value.
10.153 The other matter of interest is that, regardless of the initial value, the electron density in the daytime will have decreased to 103 electrons/cm3 within an hour (or so). This fact is apparent from Fig. 10.151 or it can be derived from equation (10.150.1). It follows, therefore, that significant degradation of HF or radar systems as the result of ionization by prompt radiation will not persist for more than an hour or so in the daytime. At night, decay is faster, as is apparent from equation (10.150.2), and effects on electromagnetic waves of the prompt radiations can usually be neglected. As will be seen later, the effects of the delayed radiation may persist for longer times.
RATE OF ELECTRON PRODUCTION BY DELAYED RADIATIONS
10.154 The rate of energy emission as delayed (beta and gamma) radiation from the radioactive residues of a nuclear explosion, consisting mainly of fission products but including activity induced by neutrons in the weapon material (§ 9.32), is represented by
where $I_t$ is the rate of energy emission at $t$ seconds after the detonation and $I_1$ is the value after 1 second.7 The total beta and gamma energy emitted is obtained (approximately) by integrating between zero time and infinity; thus,
\[ \text{Total energy } = \int_0^\infty I_1 (1 + t)^{-1.2}dt = 5I_1. \]The fraction of the delayed radiation energy emitted per second at time t is then
\[ \frac{I_1 (1 + t)^{-1.2}}{5I_1} = 0.2 (1 + t)^{-1.2}. \]10.155 About 7 percent of the fission explosion energy is radiated as delayed beta particles and gamma rays, with approximately half carried by each kind of radiation. Hence, for an explosion of $W_F$ kilotons fission yield, roughly $0.007 (1 + 1)^{-1.2}W_F$ kilotons of energy per second are radiated by beta particles and the same amount by gamma rays.
10.156 The rate of production of ion pairs (and hence of electrons) by delayed gamma rays can be estimated from an expression similar to that used to determine the electron density arising from the prompt radiation. Thus, if $kW$ in equation (10.142.1) is replaced by $0.007 (1 + 1)^{-1.2}W_F$, the result, assuming a point source for the gamma rays (cf. § 10.138), is
where $q_\gamma(t)$ cm-3sec-1 is the electron production rate at time $t$ seconds after the nuclear detonation, as observed at a slant distance $D$ miles at an altitude of H miles (see Fig. 10.140). The function $F(M)$ can be obtained from Fig. 10.142 with M defined by an equation similar to equation (10.140.1), except that the detonation altitude $H_0$ is replaced by the debris altitude $H_D$.
10.157 The radial motion of the beta particles is largely prevented by the geomagnetic field lines. The area of the D-region at an altitude of 40 miles where the beta ionization occurs is then approximately the same as the area of the debris (Fig. 10.47). If the latter rises above 40 miles, roughly half of the energy is deposited in the local D-region and half at the magnetic conjugate. The total area over which the beta-particle energy is deposited is thus twice the debris area. If the debris is assumed to be uniformly distributed over an area $A$, which may be taken to be $\pi R^2$, where $R$ is the debris radius, the electron production rate from ionization due to beta particles in each D-region is then
where φ is the local magnetic dip angle and $A$ is in square miles. The change in the numerical factor (by 4π) arises from the replacement of the area $4\pi D^2$ in equation (10.156.1) by $2A$ in equation (10.157.1) and sin φ is required because of the motion of the beta particles along the field lines. The function $F(M)$ is evaluated from Fig. 10.142 for where $H_D$ is the debris altitude in miles; in this expression the curvature of the earth is neglected.
10.158 In order to use equations (10.156.1) and (10.157.1) it is necessary to know the altitude, $H_D$, and radius, $R$, of the weapon debris. Determination of these quantities requires an understanding of the processes taking place as the debris cloud rises and spreads horizontally. The actual processes are very complex, but a simple model which parallels the gross features of the debris motion has been developed. The debris height and radius, as they change with time, for various burst altitudes as obtained from this model are shown in Figs. 10.158a, b, and c, for energy yields of 10 and 100 kilotons and 1 megaton, respectively. For interpolation between these yields, W1/3 scaling may be used, at least for the first few minutes after the explosion. The extreme left-hand end of each curve indicates the altitude of the explosion and the initial size of the fireball. It should be noted that when using Figs. 10.158a, b, and c that $W$ is the total energy yield of the explosion. For thermonuclear weapons, the fission yield $W_F$ in equations (10.156.1) and (10.157.1) is generally taken to be half of the total yield.
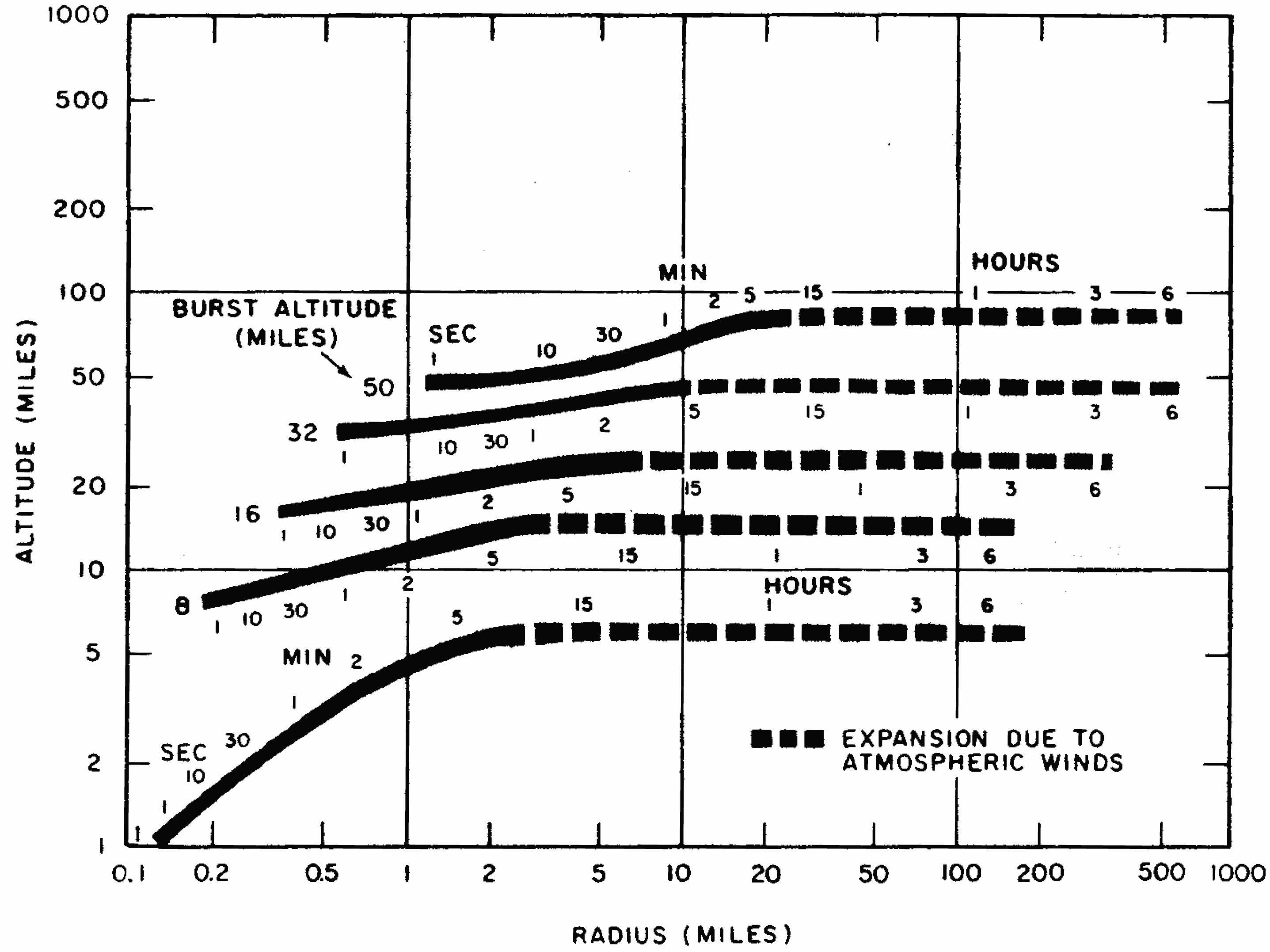

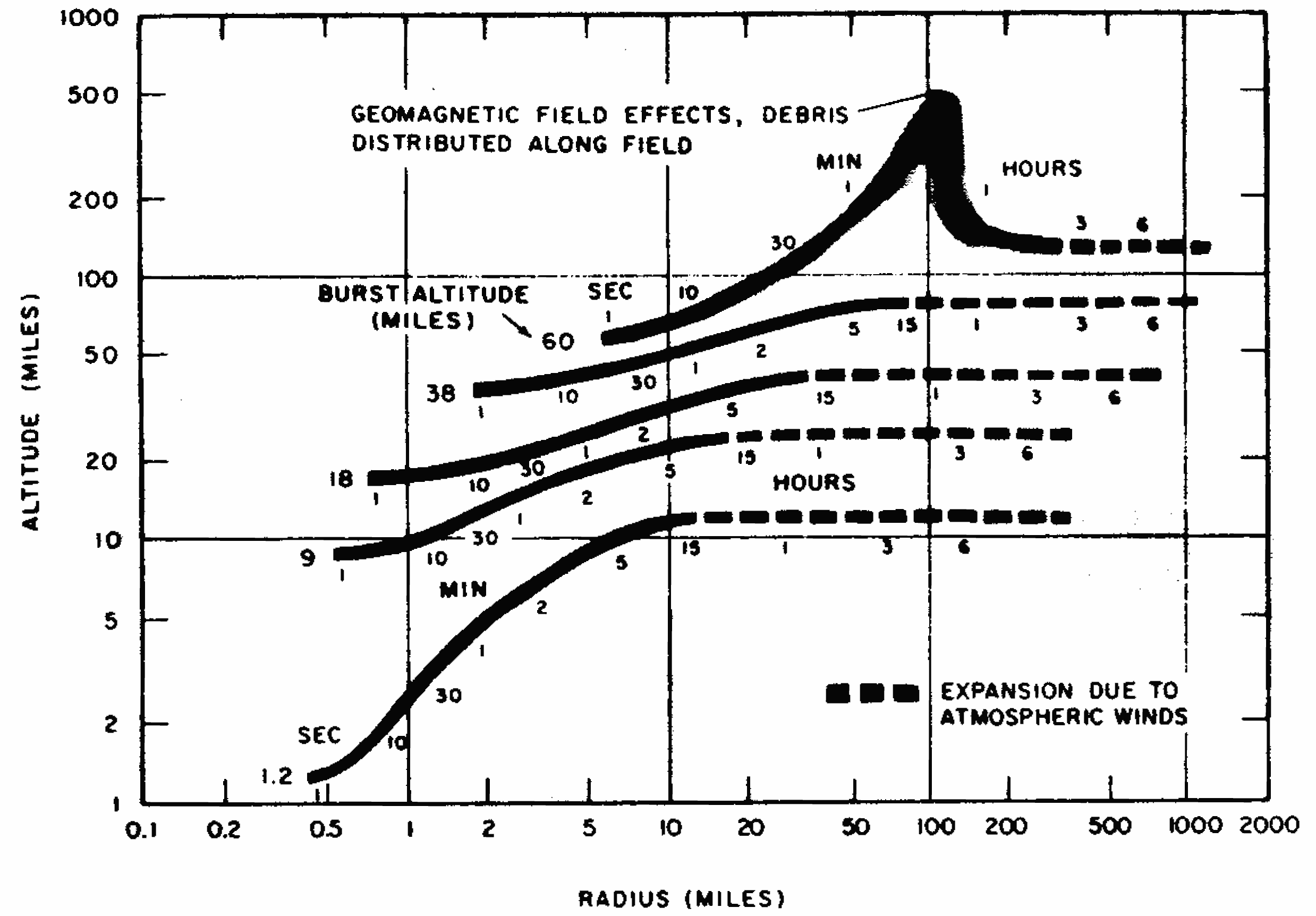
ELECTRON DENSITIES FROM DELAYED RADIATIONS
10.159 The actual electron density, $N_e(t)$, arising from the delayed radiations at a particular location and time can be calculated by assuming that, soon after the detonation, a transient steady state exists at any instant. The value of $N_e(t)$ is then obtained by equating $q_\beta(t)$ or $q_\gamma(t)$ at any time to the rate of loss of electrons by various recombination and attachment processes. The curves in Figs. 10.159a and b, for delayed beta particles and gamma rays, respectively, were obtained in this general manner for an altitude of 40 miles, where maximum attenuation of electromagnetic signals due to ionization from delayed radiations occurs both during day and night. In computing the curves, an accurate treatment for the energy spectra of the radiations was used to evaluate the rate of formation of electrons; removal rates were calculated along the lines indicated in § 10.145 et seq., with detailed consideration of all important loss mechanisms. The values shown in Fig. 10.159a were computed for a magnetic dip angle of 60°; however, they provide reasonable estimates for dip angles between about 45° and 75°, i.e., for mid-latitudes.
10.160 The curves in Fig. 10.159a for the electron density resulting from ionization by delayed beta particles are based on the assumption that the debris has risen above 40 miles. The particle energy is then equally distributed between the local D-region and the one at the magnetic conjugate. The electron densities given in the figure are those to be expected at the 40-mile altitude in each region. If the debris is below 35 miles, the delayed beta particles cause essentially no ionization in the D-region (§ 10.45); at altitudes of 35 through 40 miles, the ionization in this region is intense, but the electron densities are difficult to calculate. Because beta particles follow the geomagnetic field lines, the ionization they produce at any altitude is not affected by the earth's curvature. Gamma rays, on the other hand, travel in straight lines and may be so affected (§ 10.162).
10.161 The stopping altitude for the delayed gamma rays is about 15 miles; hence, the results in Fig. 10.159b are applicable only if the debris rises above this altitude. The principal source of error in the figure is that the gamma rays are assumed to originate from a point source at the center of the debris cloud. Since the atmospheric absorption of gamma rays is negligible above the stopping altitude, the straight-line path from the debris to the point of interest in the D-region (40 miles altitude) can lie in any direction, provided it does not pass through the stopping altitude.
10.162 As a consequence of the curvature of the earth, the path of the gamma rays, for sufficiently large distances, may intersect the stopping altitude, even when the debris rises above 15 miles. If this occurs, the energy of the gamma rays will be largely absorbed. For the conditions in Region 1 of Fig. 10.162, the straight line from the debris (center) to the observation point at 40 miles altitude does not intersect the stopping altitude for gamma rays, and the electron densities in Fig. 10.159b are applicable. But in Region 2, most of the rays will intersect a volume of air below the stopping altitude before reaching the point of interest. As a result of the gamma-ray absorption, the electron densities will be substantially below those given in Fig. 10.159b. In the intermediate (unshaded) region of Fig. 10.162, part but not all of the gamma rays will encounter the stopping altitude and the electron densities will be somewhat lower than in Fig. 10.159b. When using this figure to determine the expected effects of a nuclear explosion on a radar system, for example, a conservative approach would be to assume that the unshaded portion in Fig. 10.162 is part of Region 1 for the user's radar, but that it is part of Region 2 for the opponent's radar.

10.163 As for prompt radiations (§ 10.149 et seq.), an approximate solution to the problem of calculating electron densities arising from the delayed radiations, which is consistent with Figs. 10.159a and b, can be obtained by using the equal alpha approximation to determine the loss rate at any instant. The result can be written in the form
where $q(t)$ is either the value for beta particles from equation (I0.157.1), or for gamma rays from equation (10.156.1); the coefficients $a$, $S$, and $K$ have the same significance as before. By using the appropriate values of these coefficients for different altitudes, it has been found that the electron densities peak around an altitude of 40 miles for both daytime and nighttime conditions for slant distances more than 30 miles from the burst point. This is also the altitude for the maximum attenuation of electromagnetic signals by the ionization from delayed radiations (§ 10.159). For smaller distances from the burst point, the electron density peaks near the altitude of the debris region.
10.164 For electron production rates less than 106 electrons cm-3 sec-1, equation (10.163.1), with the values of a, S, and K given in Table 10.150 for an altitude of 40 miles in the daytime, reduces to
\[ N_e(t) \text{ at 40 miles } \approx 10^3 \sqrt{} q(t)\text{cm}^{-3} \text{ (daytime).} \]At night, the values of a, S, and Kat an altitude of 40 miles are 3 × 10-8, 0, and 0.8, respectively, and then
\[ N_e(t) \text{ at 40 miles } \approx q(t)\text{cm}^{-3} \text{ (nighttime),} \]for production rates less than about 106 electrons cm-3 sec-1. For production rates of about 107 (or more) electrons cm-3 sec-1 , the electron density at 40 miles is given approximately by
\[ N_e(t) \text{ at 40 miles } \approx 3 \times 10^3 \; \sqrt{}q(t) \text{ cm}^{-3}. \]for both daytime and nighttime. This result is consistent with Figs. 10.159a and b, in which the curves for day and night coincide when the circumstances are such as to lead to high electron densities. The conditions of applicability of these figures, as described in § 10.160 et seq., also apply to the expressions given above.
BIBLIOGRAPHY
- , “The Argus Experiment,” J. Geophys. Res. 64, 869 (1959).
- , “Decay of Ionization Impulses in the D and E Regions of the Ionosphere,” J. Geophys. Res., 68, 2167 (1963).
- , “Ionization Loss Rates Below 90 km,” J. Geophys. Res., 65, 1117 (1960).
- , “A Note on the Cause of Sudden Ionization Anomalies in Regions Remote from High-Altitude Nuclear Bursts,” J. Geophys. Res., 66, 35 (1961).
- , “Disturbances in the Ionospheric F-Region Following a Johnston Island Nuclear Explosion,” New Zealand J. Geol. and Geophys., 2, 634 (1959).
- , “Ionospheric Radio Propagation,” National Bureau of Standards, Monograph 80, April 1965.
- , “United States High-Altitude Test Experiences,” University of California, Los Alamos Scientific Laboratory, October 1976, LA–6405.
- Journal of Geophysical Research, Special Issue on the Artificial Radiation Belt, 68, 605 et seq. (1963).
- , “Introduction to the Effects of Nuclear Explosions on Radio and Radar Propagation,” General Electric Co., TEMPO, December 1967, DASA–1940.
- , “Detection of Ionization Effects from Nuclear Explosions in Space,” J. Geophys. Res., 68, 1643 (1963).
- New Zealand Journal of Geology and Geophysics, Special Nuclear Explosions Issue, 5, 918 et seq. (1962).
- Proceedings of the IEEE, Special Issue on Nuclear Test Detection, 53, 1813 et seq. (1965).
- , “Radio Noise Anomalies in August 1958,” J. Geophys. Res., 68, 2719 (1963).
- , “Introduction to Radar Systems,” McGraw–Hill Book Company, 1962.
- , “Photographs of the High-Altitude Nuclear Explosion TEAK,” J. Geophys. Res., 65, 545 (1960).
ENDNOTES
- 1 As used in this chapter, the term “electromagnetic wave” refers to radiations of wavelength of 1 millimeter or more, such as are used in radio and radar, and not to the entire spectrum described in § 1.74 et seq. [ref. § 10.05] X
- 2 A hydrodynamic disturbance of the atmosphere is a direct result of the shock wave. The air is ionized and so its motion is affected by the earth's magnetic field. The combination of hydrodynamic and magnetic effects leads to hydromagnetic (or magnetohydrodynamic) disturbances. [ref. § 10.26] X
- 3 The remaining sections of this chapter may be omitted without loss of continuity. [ref. Section 5] X
- 4 The quantity 10-2√Ne megahertz or, more exactly, $(4\pi N_ee^2/m)^½$ radians per second, is called the “critical frequency” or “plasma frequency” of an ionized medium, i.e., a plasma. It is the frequency for which the index of refraction of the given medium is zero. It is also the lowest frequency of an electromagnetic wave that can penetrate into the medium, and then only for normal incidence, i.e., for $i = 0$. [ref. § 10.134] X
- 5 The mass absorption coefficient is similar to the mass attenuation coefficient defined in § 8.100, except that it involves the energy absorption coefficient, referred to in the footnote to equation (8.95.1). [ref. § 10.138] X
- 6 The term “horizontal distance,” as used here and later, refers to the distance parallel to the earth's surface. [ref. § 10.143] X
- 7 For times that are long in comparison with 1 second, equation (10.154.1) reduces to the same form as equation (9.147.1). [ref. § 10.154] X
- 8 It is assumed that the debris expands uniformly about a stationary center once it has ceased to rise. Motion of the debris caused by atmospheric winds introduces many uncertainties in the prediction of ionization at times more than a few minutes after the burst. [ref. § 10.159 aside] X